Exploring Linked Loops in Algebraic Topology
Written on
Chapter 1: Introduction to Linked Loops
In this chapter, I aim to share some intriguing introductory concepts I recently discovered in the field of algebraic topology. This discipline focuses on converting intricate geometric challenges into simpler algebraic equations. To begin, let's examine a straightforward yet engaging problem that most individuals can grasp, even if it isn't immediately clear how to resolve it. As a child, I was fascinated by magicians who could separate two linked metal rings without breaking them. This seemingly impossible trick raises an interesting question: is there a mathematical framework that can elucidate this phenomenon?

Consider the illustration above. If we view the two interconnected loops depicted in the diagram, is it feasible to find a smooth mapping that unlinks them? More technically, can we establish a continuous mapping that transforms one loop into the other? From a mathematical standpoint, we can represent these linked loops as two circles in R³, which can be visualized as a union of two rings embedded in three-dimensional space.
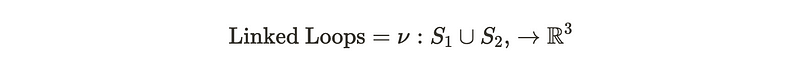
Using standard Cartesian coordinates, we can express these loops explicitly. Below, the two circles are represented in the z-plane and y-plane, respectively. If you plot them, you'll notice that the circles are indeed linked together.
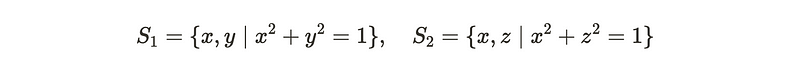
Alternatively, we can interpret the two linked circles as an embedding within R³. I will delve deeper into the rationale behind this perspective in a subsequent chapter. The two linked loops can be viewed as an embedding of two circles into R³. Embeddings are defined as continuous and injective mappings, providing a more refined way to analyze the loops through the lens of mappings.
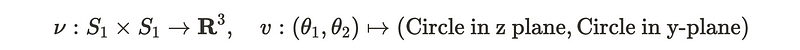
A homeomorphism, defined as a continuous mapping with a continuous inverse, raises the question: is there a homeomorphism connecting this embedding to two unlinked circles? To explore this, we must investigate intermediate spaces, which will be elaborated upon in the following sections.
Section 1.1: Unlinked Circles
In contrast, two circles that are not linked can be represented as the union of two sets as depicted below. The first set represents a standard circle, while the second set is an identical circle, slightly translated to the right to ensure they do not overlap.
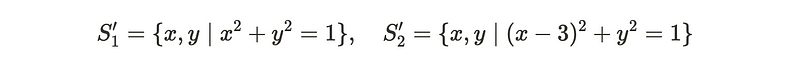
The question arises: can we create a continuous mapping from the linked circles to this unlinked configuration? This inquiry parallels the concept of extensions. An extension in mathematics involves mapping to an intermediate space to facilitate problem-solving. Here, we observe a continuous extension from the two loops to two discs, and subsequently back into R³. For simplicity, let's consider a single circle.
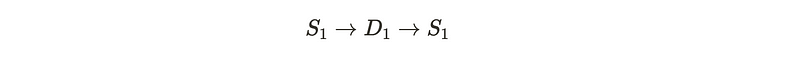
The initial mapping from the circle to the disc is known as the inclusion map. The second mapping poses a more complex question: is there a continuous, surjective mapping from the disc back to the circle? The answer is affirmative. One can represent any point on the circle using coordinates x and y. To map this back to the circle, you can exponentiate the x-coordinate, effectively creating a mapping into the circle. This mapping is both surjective and continuous.
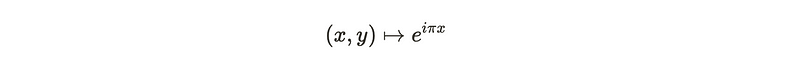
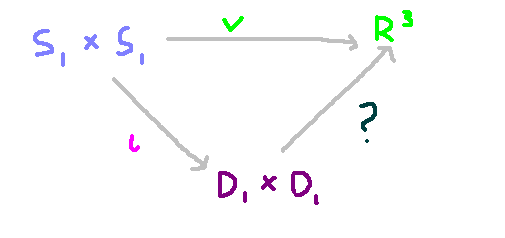
With these considerations, it becomes evident that a smooth mapping from the disc back into the circles in R³ exists, showcasing a factorization of mappings represented as follows. The upper mapping, denoted by v, illustrates the original embedding, while the mapping from circles to discs represents the inclusion map. This approach simplifies problem-solving, as working with functions often proves less challenging than dealing with geometric shapes.
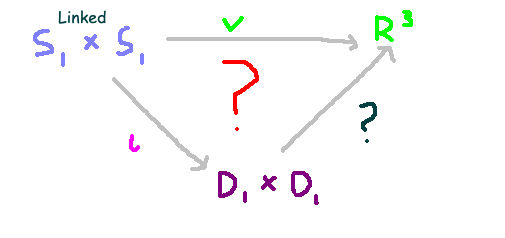
Are They Equivalent?
To determine if these mappings indeed yield the same results, we need to examine whether a similar process applies when the embedding consists of two linked discs instead of two unlinked discs. Through algebraic techniques, we find that this transformation is, in fact, impossible.
References
A tutorial on creating linked loop friendship bracelets, showcasing techniques that mirror the mathematical principles discussed.
An instructional video on the linked loops stitch in crochet, illustrating practical applications of linked loop concepts.