Exploring the Intricacies of Leibniz' Rule in Calculus
Written on
Chapter 1: Introduction to Calculus and Leibniz' Rule
Calculus is a prominent field in mathematics, often emphasized in educational curricula through topics like differentiation and integration. However, this article aims to introduce a compelling concept: Leibniz’ Rule, which marries differentiation and integration to reveal intriguing findings. We will start with some foundational analysis before transitioning into captivating applications.
To begin, let's establish a function described as follows:
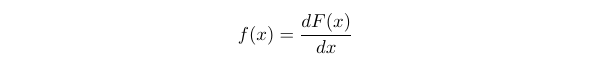
From this function, we derive:
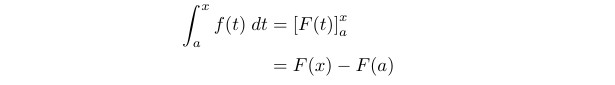
(1.1)
By applying differentiation with respect to ( x ) on both sides of (1.1), we arrive at:
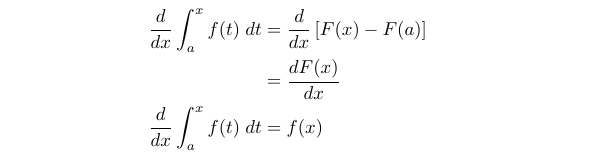
(1.2)
Using similar logic, we can also express the following:
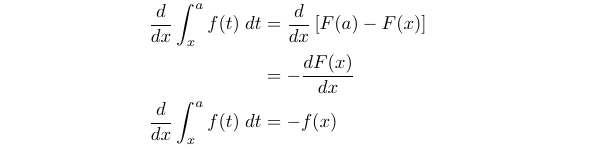
(1.3)
Suppose we wish to determine ( frac{dI}{dx} ) where:
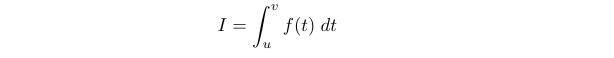
According to the chain rule for functions with multiple variables, we can express:
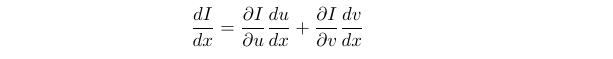
(1.4)
Now, if we substitute ( x ) with ( u ) and ( v ) in (1.2) and (1.3), treating ( u ) as a constant due to the nature of partial derivatives, we find that ( frac{partial I}{partial v} ) corresponds to the result from (1.2):
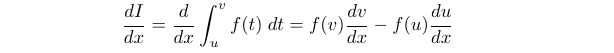
(1.5)
Let’s now define ( I ) as follows:
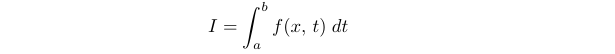
where ( a ) and ( b ) are constants. Our goal is to compute ( frac{dI}{dx} ), a specific instance of Leibniz’ Rule. We can state Leibniz' Rule without proof as:
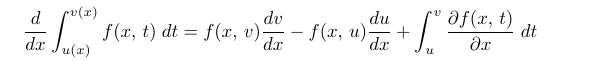
Leibniz’ Rule states that if ( v(x) = b ) and ( u(x) = a ), then ( frac{dv}{dx} = frac{du}{dx} = 0 ), leading us to:
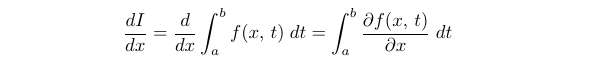
This principle will be pivotal in our forthcoming exercises.
Chapter 2: Application of Leibniz’ Rule
Exercise 1
We seek to evaluate the following integral for ( n geq 0, n > 0 ):
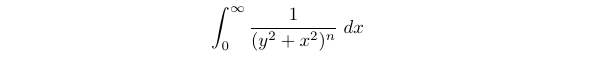
Our initial step is to assess a simpler case when ( n = 1 ). Remembering the derivative of ( text{arctan}(x) ), we find that as ( x to infty ), ( text{arctan}(x) to frac{pi}{2} ), which allows us to compute this case swiftly.
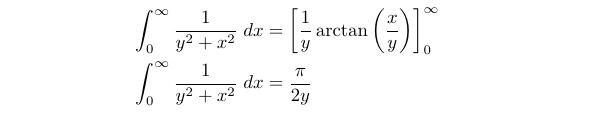
(2.1)
Here, Leibniz’ Rule comes into play. By differentiating (2.1) with respect to ( y ), we can observe the advantages of this approach.
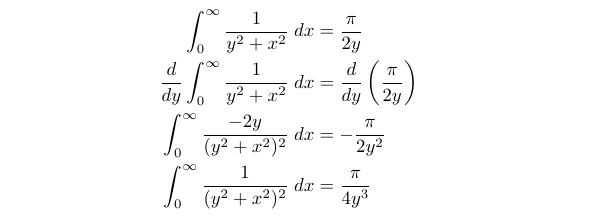
We can then intuitively hypothesize a general form for the integral and validate it through induction as follows:

Notice that we employed Leibniz’ Rule during differentiation to derive (2.1) as well as in the induction proof, which is quite elegant!
Exercise 2
Next, consider these two integrals for which we aim to determine the values:
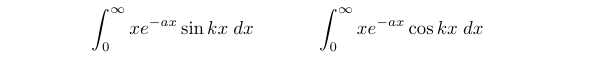
(3.1) and (3.2)
The first step involves analyzing a related integral and differentiating it with respect to ( a ) and ( k ) individually to yield the desired integrals.
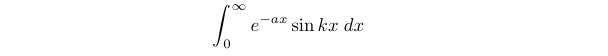
(3.3)
Some may recognize (3.3) as a Laplace transform of ( sin(kx) ), which allows us to find the integral's value immediately. However, let’s evaluate this integral using the cyclical properties of successive derivatives and integrals of ( e ) and ( sin ).
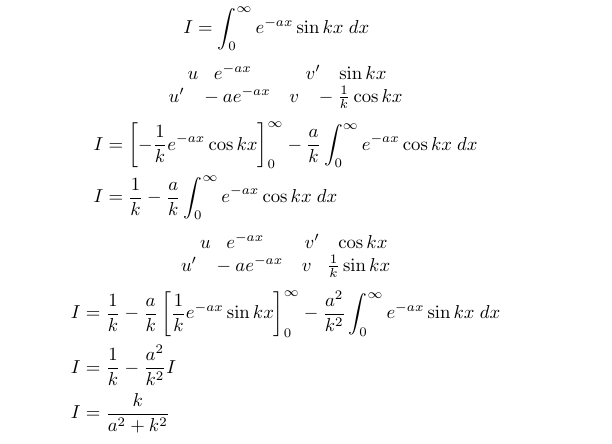
Thus, we determine the value of (3.3):
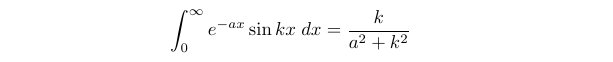
(3.4)
Next, we will apply Leibniz’ Rule in two ways. Initially, we will differentiate (3.4) concerning ( a ).
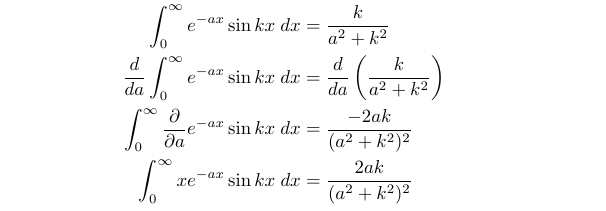
This yields (3.1). Similarly, we can derive (3.2) by differentiating (3.4) with respect to ( k ).
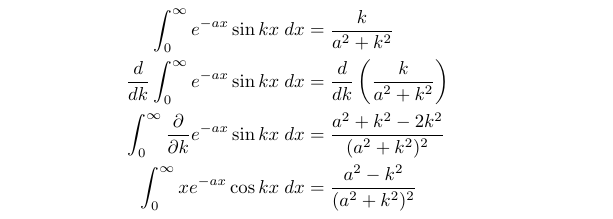
Thus, we successfully obtained both (3.1) and (3.2) utilizing Leibniz’ Rule.
Exercise 3
Finally, we will find the value of the following integral for ( n geq 0 ):
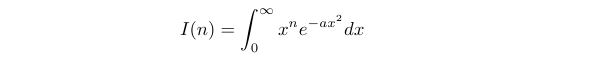
This exercise necessitates analyzing the integral for even and odd ( n ) separately. Let’s start with odd ( n ) (i.e., ( n = 1, 3, ... )). Setting ( n = 1 ) provides a straightforward base case, allowing us to evaluate the integral using elementary methods.
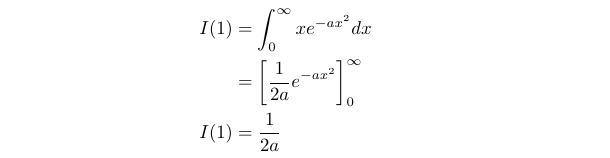
Next, we differentiate ( I(1) ) with respect to ( a ), which leads us to ( I(3) ).
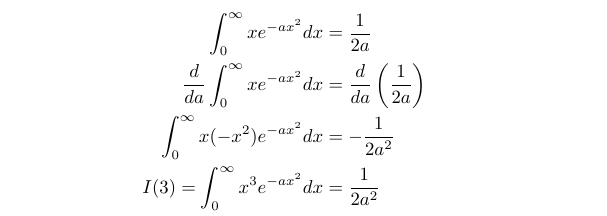
As we repeat this differentiation process with respect to ( a ), we obtain consecutive odd values for ( I(n) ). This allows us to derive a general form for ( I(2k+1) ).
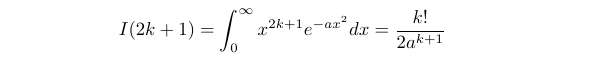
For even ( n ), we must first compute the case when ( n = 0 ) and then apply a similar approach as for odd ( n ) by differentiating with respect to ( a ). When ( n = 0 ), some may recognize that we have a Gaussian integral. I will outline the standard derivation, which involves extending into three dimensions and utilizing symmetry. Additionally, we will change variables in a double integral, including a Jacobian transformation. This aspect will be elaborated in a future article focused on multiple integral variable changes and the Jacobian.
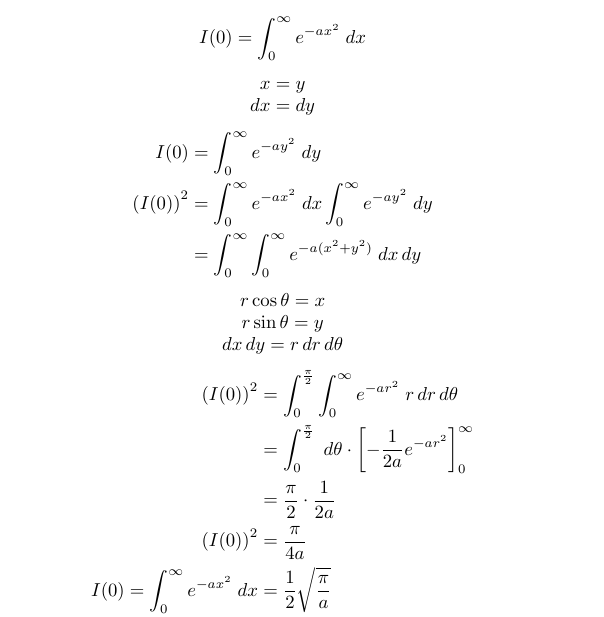
Now, with this result, we differentiate both sides with respect to ( a ) to derive the general form for ( I(2k) ).
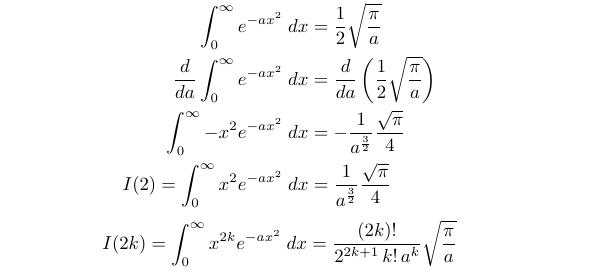
By combining these two results, we ultimately arrive at:
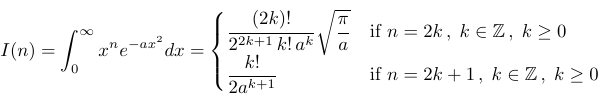
Thank you for reading! Feel free to share your thoughts on Leibniz’ Rule in the comments.