Preliminary Interpretations

I prefer the phrasing above to the more frequent alternative: we cannot measure both momentum and position simultaneously. During my undergraduate studies in quantum mechanics, I believed I had grasped this concept. A vivid image formed in my mind: measuring a particle's position disrupts its momentum, leading to a loss of precision in measurement and vice versa.

While this viewpoint holds some truth, it conveys a misleading impression. It suggests that the limitations lie with our measuring tools, implying that future advancements could allow simultaneous precise measurements. This interpretation is fundamentally flawed.

Upon reaching graduate school, I recognized that uncertainty principles are prevalent in a purely mathematical context. The Heisenberg uncertainty principle is, at its core, a mathematical truth arising from the momentum and position operators. Thus, from a theoretical standpoint, it's impossible to "know" both simultaneously, even without measurement devices.

While discussing the nature of "knowledge" could veer off-topic, it's crucial to understand that the uncertainty principle suggests it doesn't make sense to inquire about both the momentum and position of a particle. This is somewhat misleading, as we do understand the exact uncertainty involved in such attempts.

An analogy might help clarify: asking whether blue is hard or soft lacks meaning. Just as you cannot assign a hardness property to a color, you cannot formulate an equation (a wavefunction for a particle) that defines both precise momentum and position concurrently.

The Mathematical Framework

To understand the mathematical basis of this principle, we must recognize that every observable quantity (like momentum and position) is associated with a Hermitian operator. If you're unfamiliar with this concept, there's no need to worry. The essential takeaway is that "knowing" or "measuring" a specific observable state correlates with the particle's wavefunction being an eigenfunction of that operator (a definition will follow).

Consider two operators, A and B, which correspond to observable quantities a and b. If it makes sense to say we can measure properties a and b simultaneously, there exist two numbers, λ₁ and λ₂, such that:

Aψ = λ₁ψ and Bψ = λ₂ψ.

This definition describes the condition of being an eigenfunction.

The commutator of two operators is defined as the difference between the product of the two operators in different orders:

[A, B]ψ = ABψ - BAψ.

Applying this commutator to ψ leads us to:

[A, B]ψ = ABψ - BAψ

= Aλ₁ψ - Bλ₂ψ

= λ₁λ₂ψ - λ₁λ₂ψ

= 0.

This illustrates a basic fact about operators: if it is possible to simultaneously know two properties for a given function (or distribution), the commutator applied to that function yields zero.

Thus, it becomes nonsensical to inquire about both properties if the commutator has no (non-trivial) kernel.

Now, regarding the Heisenberg uncertainty principle in quantum mechanics, we need only compute the commutator of the momentum and position operators to confirm that it has no kernel (except for the zero function, which does not represent a valid wavefunction).

For verification, the position operator is defined as xψ = xψ, while the momentum operator is pψ = -iħ(d/dx)ψ.

Now let’s compute:

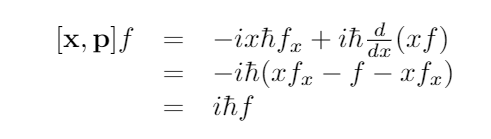
This computation shows that the commutator results in a constant multiplied by the identity operator, which can never equal zero! Therefore, it is illogical to expect to know both the position and momentum of a particle at the same time. There isn't even a theoretical particle construct that possesses this characteristic.

It’s essential to highlight this fact, as there are operators for which simultaneous knowledge of two properties is often impossible, yet special particles may still allow for it.

This also indicates that various other mathematical uncertainty principles can be derived by examining different operators. A well-known example is the Fourier transform, which reveals a fundamental uncertainty in knowing both frequencies and temporal localization.

Key Takeaways

The Heisenberg Uncertainty Principle is not merely about quantum peculiarities or the observer effect collapsing the wavefunction. It does not stem from flawed measurement tools or the act of measuring altering the particle. Rather, uncertainty principles are prevalent throughout mathematics, and as illustrated, they represent a purely mathematical phenomenon associated with operators. This understanding offers one of the more enlightening interpretations of the concept.