Chapter 1: Introduction to Neural Networks

Neural networks are fascinating constructs, particularly the perceptron, which serves as a binary classifier and represents one of the earliest forms of these systems. Understanding the mathematical foundations behind experimental AI and neural networks can be daunting, but it need not be. Personally, I find that clear illustrations and straightforward language are the most effective ways to grasp complex topics. For instance, I previously created an illustrated guide to Neural Networks that simplifies these concepts.

Building a Basic Neural Network

What is our objective? We aim to develop a straightforward neural network that can be trained to recognize specific patterns.

In the realm of AI research, the landscape is often dominated by academic publications and mathematical rigor. My focus lies in experimental AIs grounded in neuroscience, although there is considerable overlap with established AI principles. This guide will lead you from abstract ideas and concepts to their mathematical representations, accompanied by code examples for practical implementation.

Getting Started

From a high-level perspective, the brain consists of semi-discrete units called neurons—approximately 86 billion of them—along with their countless connections, numbering in the hundreds of trillions. This intricate network serves as the basis for neural computation and every action we perform.

Groups of neurons can be illustrated in several ways:

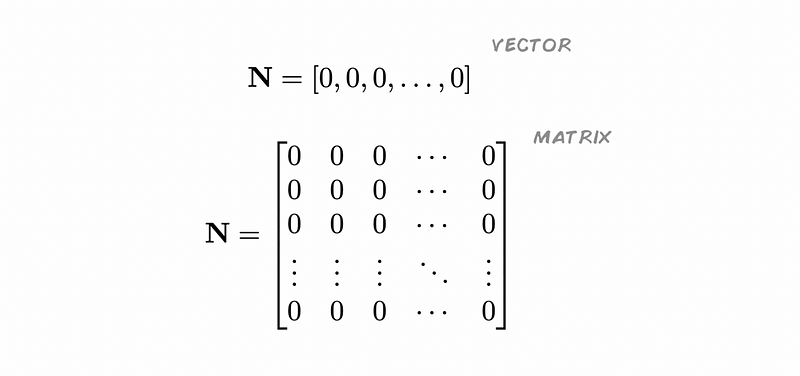
For now, envision each zero as an unactivated neuron. While vectors can be effective for basic neuron groupings and quick computations, a more complex field of neurons is better represented using a matrix.

# Vector:

num_neurons = 10

neuron_list = [0] * num_neurons

print("Neuron list:", neuron_list)

# Neuron list: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

# Matrix:

import numpy as np

num_rows = 4

num_cols = 4

neuron_matrix = np.zeros((num_rows, num_cols))

print(neuron_matrix)

# [[0. 0. 0. 0.]

# [0. 0. 0. 0.]

# [0. 0. 0. 0.]

# [0. 0. 0. 0.]]

It's worth noting that the preferred approach for handling groups of neurons is through multidimensional arrays, also known as tensors. This can seem intimidating initially:

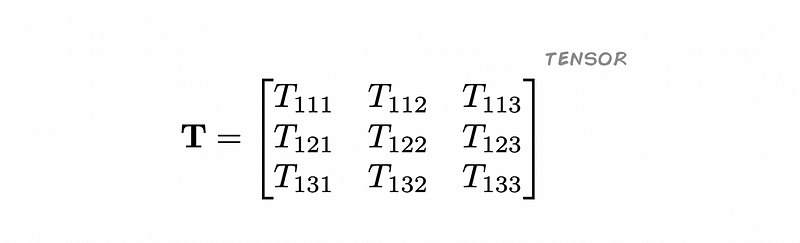
This 3D tensor has dimensions of 3x3x3, with each element represented by indices i, j, and k, where each can range from 1 to 3. Like many technological constructs, our methods do not always mirror nature’s design; for example, airplanes do not fly by flapping their wings.

Encoding Information

Neurons transmit action potentials, which encode information and perform computations. Although the latter is still not fully understood, we can concentrate on encoding for now.

Binary coding can simply represent the on/off states of neurons, indicating whether they are firing or silent. Continuous coding can represent varying levels of neuron responses. Both biology and AI/ML utilize these codes in numerous combinations for data representation, computation layers, and more, leading to diverse outcomes.

To better understand tensors, consider what a multidimensional tensor or vector signifies. The brain does not possess a singular neuron field that captures all dimensions of reality, such as color, sound, or temperature; rather, it has specialized neuron fields for each dimension, which can be integrated to form new representations.

A tensor can unify these stimuli into a neat multidimensional representation, as illustrated by this 3D tensor, which can be equivalent to a combined vector (1D tensor) and a 2D matrix.

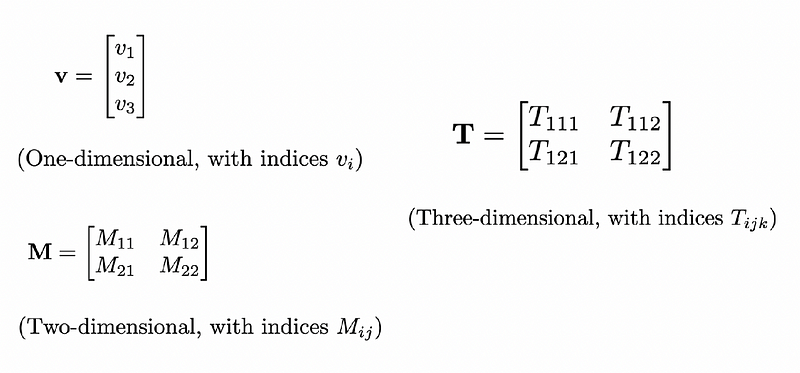
Understanding Connections and Weights

To describe connections between neurons, a connectivity matrix can be employed, where each element indicates the connection status between two neurons across multiple fields. A weight matrix may also be used to represent graded connections.

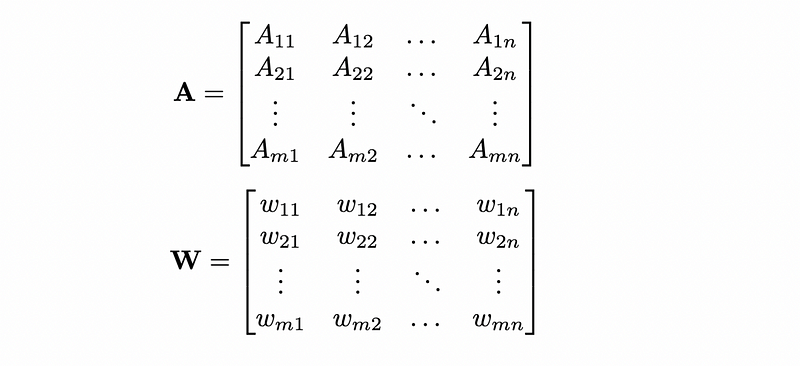
Another popular method for describing connections is through graphs, or by characterizing functional connectivity among neuron fields, which is how most AI layers function.

import numpy as np

import matplotlib.pyplot as plt

# Generate a random connectivity matrix with weights

num_neurons_field1 = 10

num_neurons_field2 = 10

connectivity_matrix = np.random.rand(num_neurons_field1, num_neurons_field2)

# Plot the connectivity matrix as a heatmap

plt.figure(figsize=(8, 6))

plt.imshow(connectivity_matrix, cmap='viridis', interpolation='nearest')

plt.colorbar(label='Connection Strength')

plt.title('Connectivity Matrix')

plt.xlabel('Neurons in Field 2')

plt.ylabel('Neurons in Field 1')

plt.show()

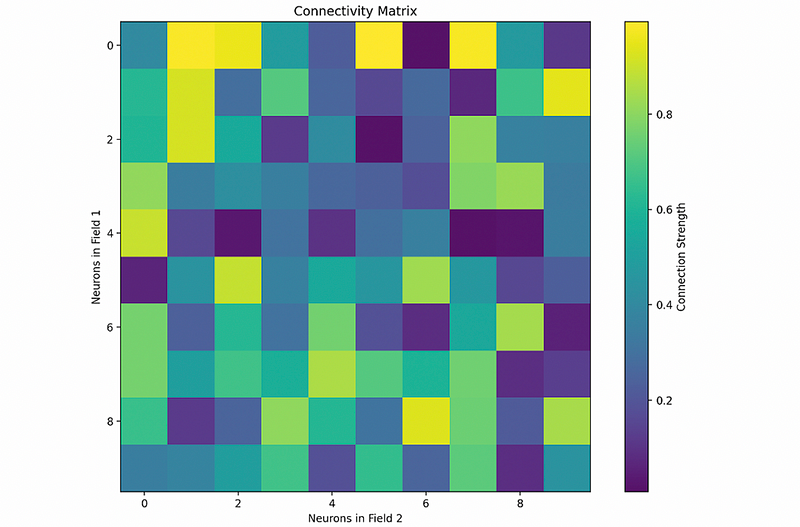
Dynamics of Neuron Functionality

Understanding neuron fields and their connections also requires examining their behavior over time. Both the brain and AI systems rely on specific interactions and computations among neuron fields, such as adjusting connection weights, which ultimately lead to behavior and functionality.

Hebbian Learning, summarized as "Neurons that fire together, wire together," is one process that can be formalized:

Suppose we have binary response neurons (0-1) and a learning rate of n=1. In this case, the connection weight between neurons i and j should increase by 1 when they are simultaneously active.

import numpy as np

# Define the activities of neurons in Field 1 and Field 2

x_field1 = np.array([[1, 0],

[0, 1]])

x_field2 = np.array([[1, 1],

[1, 0]])

# Define the initial connection weights

weights = np.array([[0.0, 0.0],

[0.0, 0.0]])

# Define the learning rate

learning_rate = 1

# Compute the product of the neuron fields

product = np.multiply(x_field1, x_field2)

# Apply the weights

delta_weights = learning_rate * product

# Update the connection weights

weights += delta_weights

# Print the updated connection weights

print("Updated Connection Weights:")

print(weights)

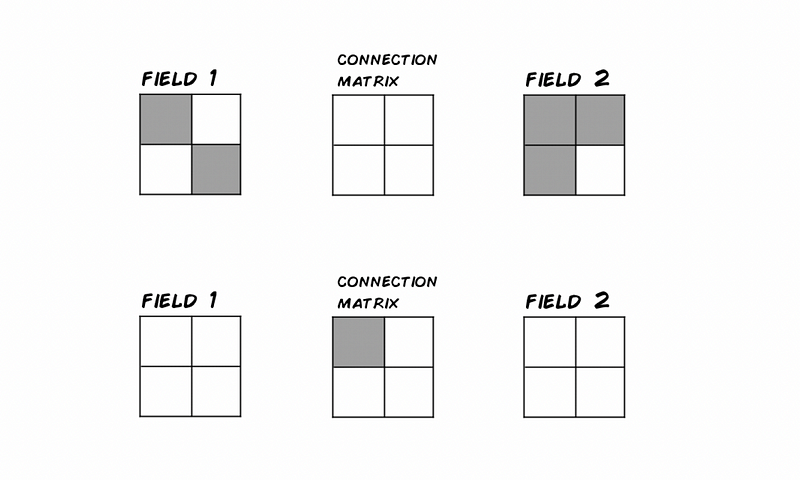
After training this minimal neural network, the neurons that activated together are now connected due to the Hebbian Learning rule.

The Importance of Matrices

Understanding matrices is crucial for working with AIs and neural networks. Familiarizing yourself with their operations and how to implement them in code is beneficial.

You may also want to model specific behaviors in the brain or replicate them in an AI context, such as the firing rate of a neuron:

Incorporating models might be more accurate when creating objects that perform computations. For instance, here is a neuron object that implements firing rate functionality:

import numpy as np

class Neuron:

def __init__(self, threshold, modulation):

self.threshold = threshold

self.modulation = modulation

def firing_rate(self, input_current):

return 1 / (1 + np.exp(-(input_current - self.threshold) / self.modulation))

# Define the parameters for the neuron

threshold = 0.5 # Example threshold

modulation = 0.1 # Example modulation

# Instantiate a Neuron object

neuron = Neuron(threshold, modulation)

# Define the input current

input_current = 0.8 # Example input current

# Compute the firing rate using the Neuron object

rate = neuron.firing_rate(input_current)

# Print the firing rate

print("Firing Rate:", rate)

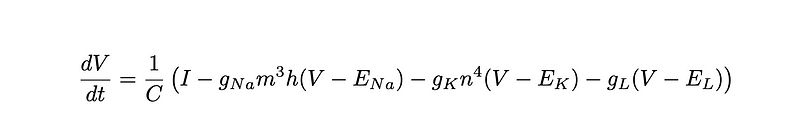
Exploring Advanced Concepts

This overview touches on the essentials, but it merely scratches the surface. The following equations and topics delve deeper into both biological neural networks and artificial intelligence, which you can explore based on your interests or projects.

The Hodgkin–Huxley model, illustrated here, describes action potentials and may seem complex, but it essentially states that changes in membrane potential (dV over time dt) are influenced by various cellular elements over the cell's capacitance (C).

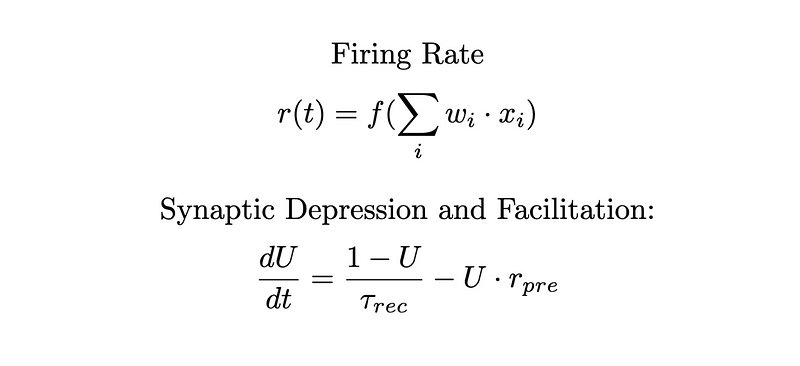
Conclusion

While these examples capture fundamental aspects of neural activity, the real challenge lies in synthesizing and simplifying these components into larger models that accurately reflect the complexities of neural networks.

Artificial Intelligence and Machine Learning concepts related to neural networks also require a solid understanding of what you are representing. For instance, the feedforward equation transforms a vector (x) using weights (W) and biases (b) to produce a new vector (y) in a two-layer neural network.

I hope this guide provides a clearer understanding of the basic mathematics involved in AI and neural networks, making the subject more accessible and intriguing.