Motivation for Exploration

A recent tweet I encountered piqued my interest in this topic. If you search online for "Fibonacci: From miles to kilometers," you'll uncover various discussions. However, most focus solely on the method without delving into the reasoning behind this intriguing conversion technique.

This article aims to provide a unique perspective, particularly as I plan to introduce singularities and generating functions in future writings. Thus, it's essential to establish a foundation for these upcoming topics.

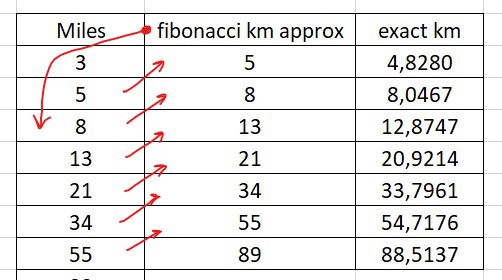
Section 1.1: Accurate Conversion Formulas

To clarify, using the Fibonacci sequence for conversion yields only an approximation and is not exact. The precise formula for converting distances is:

Distance in kilometers = 1.60934 × Distance in miles.

This means you simply multiply the distance in miles by the constant 1.60934.

Subsection 1.1.1: Fibonacci's Approximation

Interestingly, the initial observations suggest that one can approximate the conversion using the Fibonacci sequence by multiplying by 1.60934. But why does this work so effectively?

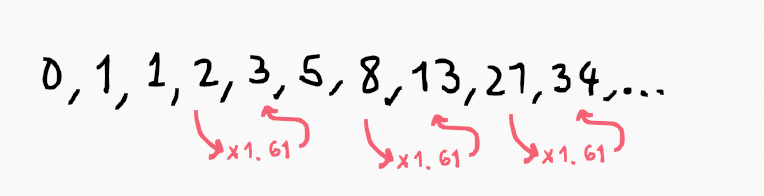
For instance, multiplying 8 by 1.60934 gives approximately 12.87472, close to 13, while 21 multiplied by the same constant yields around 33.79614, which is near 34. The question remains: why does the number 1.60934 serve as such a reliable predictor for the next Fibonacci number?

The answer lies in the concept of 'natural frequency' and the pole locations derived from the Fibonacci generating function.

Section 1.2: Understanding the Generating Function

The Fibonacci generating function stems from its defining characteristic: each number in the sequence is the sum of the two preceding numbers.

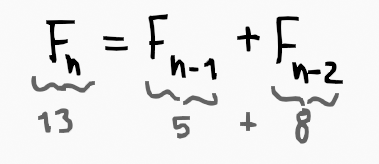
This definition holds true for every Fibonacci number. To derive its generating function, we can create a mathematical function where multiplying by 'x' represents a lag of one position in the sequence.

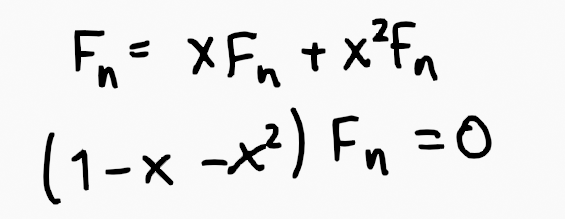
The function we focus on is its reciprocal, which helps us analyze the sequence more effectively.

Generating Function Analysis

Employing partial fractions allows us to isolate the poles, one of which corresponds to the golden ratio.

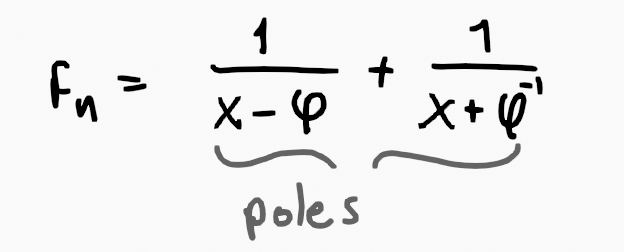
This approach leads us to Binet's formula for Fibonacci numbers. While this involves concepts related to geometric series, we'll save that discussion for another time.

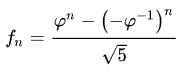
The significant takeaway here is that the golden ratio—approximately 1.61803398875—serves as one of the poles and closely resembles the conversion factor of 1.60934. The other pole approaches zero as its exponent increases.

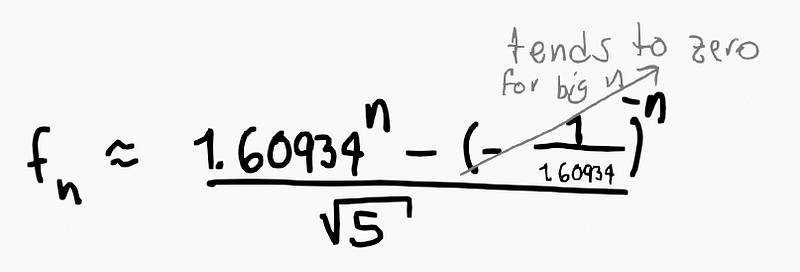
To forecast the next value in the sequence, we use the formula for f_{n+1}.

Conclusion: The Intriguing Connection

The unexpected relationship between the Fibonacci sequence and the miles-to-kilometers conversion ties back to the golden ratio. They share a common mathematical foundation. Remarkably, this ratio aligns closely with the average length of a human step in meters multiplied by 1.60934, which translates to a Roman human step measuring exactly that length.

Historically, the mile has its roots in Roman measurements, with the term deriving from the Latin "mille passuum," meaning "a thousand paces." Notably, a pace during Roman times equated to five human feet lined up from toe to heel.

1000 Steps = 1.60934 x 1000 meters, which simplifies to 1 Step = 1.60934 x 1 meter.

This first video delves into how the Fibonacci sequence can be used to convert miles into kilometers, providing a visual overview of the process.

The second video further explores the conversion from miles to kilometers using the Fibonacci sequence, enhancing the understanding of this mathematical concept.

A final note: the equation depicted with isolated poles is missing a constant (the residue), which means it is not entirely accurate. Additionally, the notation for F_n could sometimes be represented as f(x) instead. I've shared the core idea here, and I intend to elaborate on generating functions in future discussions.

Thank you for reading!