Chapter 1: The Challenge of Mathematical Proofs

Engaging in mathematical challenges can be incredibly rewarding. One such challenge involves finding at least two distinct methods to validate a mathematical statement.

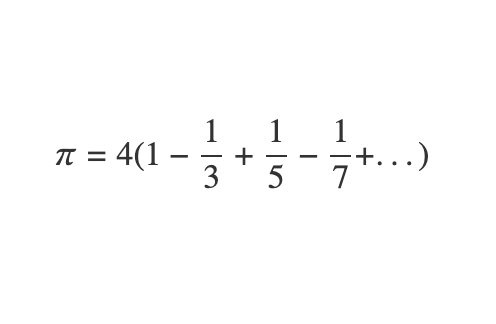
Let’s examine the expression above. To verify its accuracy, we can use Python to compute the series up to the n-th term. This will allow us to assess the difference between the mathematical constant π and our calculated series for values of n set at 100, 1000, 10000, and 1000000.

from math import pi

def pi_sum(n: int) -> float:

total = 0

for i in range(1, n + 1):

total += ((-1) ** (i - 1)) * (1 / (2 * i - 1))

return 4 * total

for n in [100, 1000, 10000, 1000000]:

print(pi - pi_sum(n))

The results show:

> 0.00999975003123943

> 0.000999999749998981

> 9.99999997586265e-05

> 1.0000000187915248e-06

This suggests that our statement holds true, as the algorithm demonstrates that our series converges to π. However, this does not constitute a definitive mathematical proof. I find great satisfaction in using mathematics to confirm truths beyond doubt. When I encounter expressions such as the one above, I challenge myself to prove it in at least two different ways.

Employing various methods to prove a concept not only sharpens your mathematical skills but also reinforces the validity of the result. Moreover, it can uncover connections between different approaches that may be useful in solving other problems. Let’s explore three distinct methods to substantiate our result.

Section 1.1: Method 1 — Integrating a Geometric Series

Consider the following expression for 0 < y < 1:

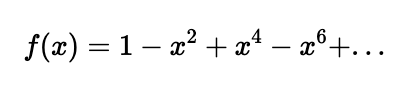
Since all values of our integral range are below 1, we can regard f(x) as a geometric series with a common ratio of (-x²) that is less than 1 in absolute value. This allows us to utilize the formula for the sum to infinity of a geometric series within our integral:

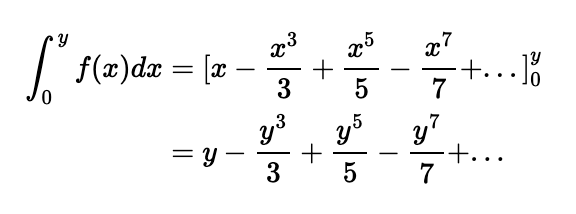
Thus, we confirm that for all positive y < 1:

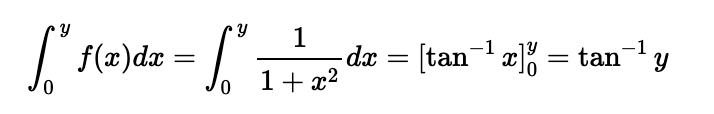
Now, by taking the limit as y approaches 1, we establish our result.

You might question why I opted to work with limits rather than simply integrating from 0 to 1. The reason is that f(1) = 1 – 1 + 1 – 1 + ... does not converge to a defined value. Statisticians may claim this sums to 1/2, but it is not accurate! This example illustrates why geometric series only converge if their common ratio's absolute value is strictly less than 1.

Section 1.2: Method 2 — A Taylor/Maclaurin Series

A Taylor series is an infinite sum expansion of a function f(x) that can be determined as long as f(x) is infinitely differentiable at a specified point. The Taylor series derived at the point x=0 is called a Maclaurin series. The Maclaurin series is defined as follows:

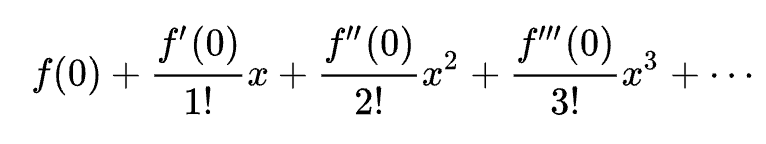
Applying this to the inverse tangent function yields the following Maclaurin series:

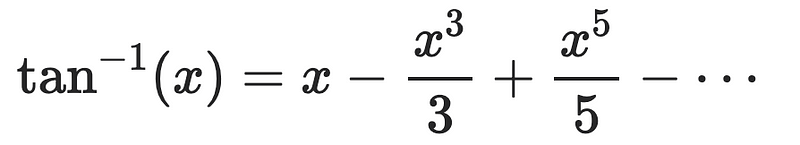
Setting x = 1 in this series provides the desired result. Notice the strong connections between this proof and Method 1—both are based on the calculus of the inverse tangent.

Chapter 2: Method 3 — A Trigonometric Integral

The final argument is more complex and differs significantly from the previous two. I will prove this statement for all positive integers n using mathematical induction.

Let:

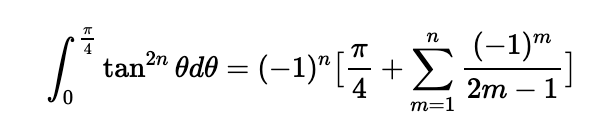
Initially, I will demonstrate that it holds true for n=1:

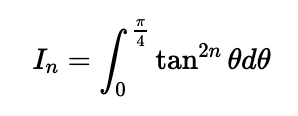
This matches our expression when n=1. Next, I will assume the expression is valid for n=k-1 and then prove it for n=k.

First, note:

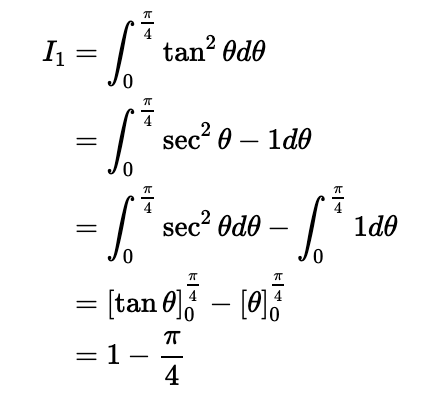
Now, we will apply a classic substitution. Let u = tan(θ). Then, du = sec²(θ)dθ, leading us to:

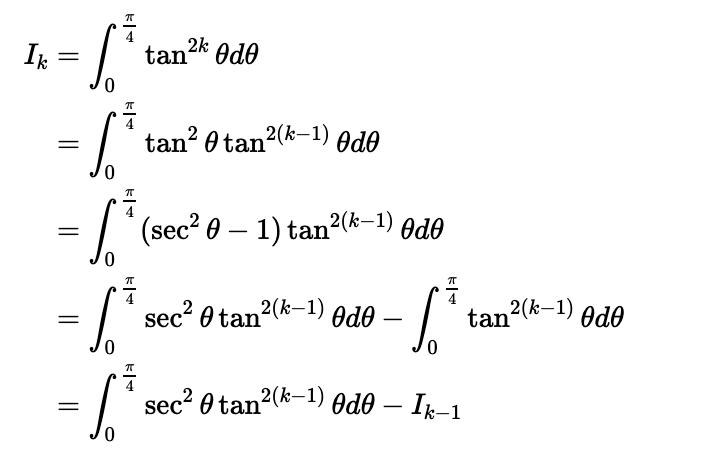
Assuming our expression for n=k-1, we complete the proof:

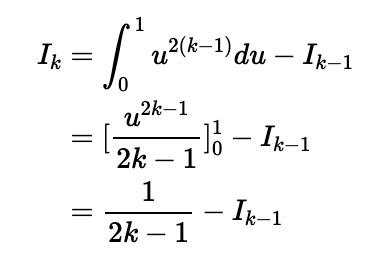
This concludes our proof (the last step can be verified by checking cases for even and odd k).

Why is this useful? Notice that 0 < tan(θ) < 1 when 0 < θ < π/4. As we raise tan(θ) to higher powers within this range, the values shrink. Hence, as n approaches infinity:

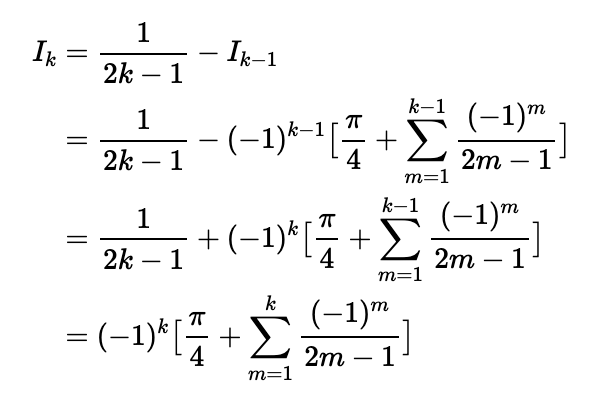
When integrating a positive function, we are calculating the area under the curve, leading us to conclude that:

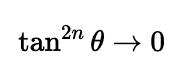
Since no power of -1 can equal zero, we must conclude that the expression in brackets equals zero, thereby confirming our result.

Challenge:

Try employing three similar arguments to find three proofs that:

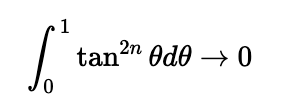
As a hint, for the third argument, consider integrating odd powers of tan(θ) and following a similar logic to observe the outcomes.

Did you enjoy exploring these diverse arguments? Do you see any mathematical connections among them? Feel free to share your thoughts!

This video explores the Love Math Challenge, transforming the challenges of learning math into joyful experiences.

Join the 30 Day Math Challenge to enhance your skills and find joy in mathematics!