Solution to the Puzzle

To tackle this calculus challenge, we start by designating point P with coordinates (a, a²).

Since y = x², we can apply the power rule to find the derivative, yielding dy/dx = 2x. Thus, at x = a, dy/dx = 2a, which represents the slope of the tangent at point P. The slope of the normal line is the negative reciprocal, given by:

text{slope of normal} = -frac{1}{2a}

Using the point-slope form of a line, we can express the equation for the normal line as follows:

frac{(a - x)}{(y - a²)} = -frac{1}{2a}

Rearranging gives us:

y = -frac{1}{2a}x + a² + frac{1}{2}

Let’s assume that the normal line intersects the parabola at point Q = (u, u²). We can find the coordinates of Q by substituting y = x² into our equation and solving for u in terms of a:

u = a - frac{1}{2a}

Next, we will utilize Desmos to visualize the problem more clearly.

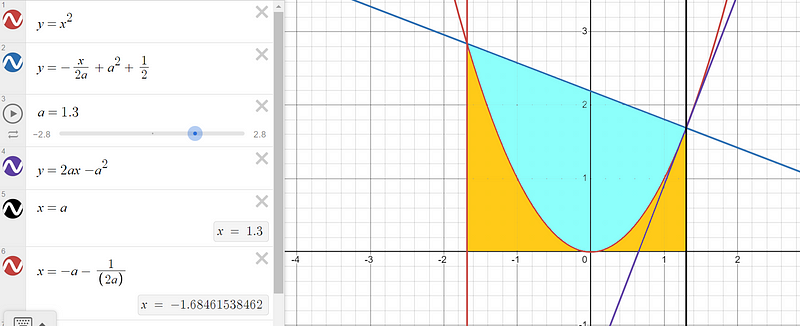
In this illustration, the blue region represents the area we aim to minimize. Vertical lines at x = a and x = a - 1/(2a) create a trapezium encompassing the blue area. The objective is to subtract the orange regions from the trapezium to derive an expression for the blue area.

Using the trapezium area formula along with integral calculus, we find that the area of the blue region can be expressed as:

text{Area} = text{Area of trapezium} - text{Area of orange regions}

You may wonder why we avoid substituting u = a - 1/(2a) into the equation too early. This approach simplifies the calculations until the end.

Next, we apply the chain rule to differentiate the area A with respect to a.

frac{dA}{da} = text{expression involving } frac{du}{da}

Now, we need to calculate (frac{du}{da}):

frac{du}{da} = -frac{1}{2a²}

The derivative dA/da equals zero when:

(1 - frac{du}{da}) = 0

Thus, our final result indicates that the area is minimized when:

text{coordinates of } P text{ yield minimal area}

Below is the graph illustrating when the area reaches its minimum!

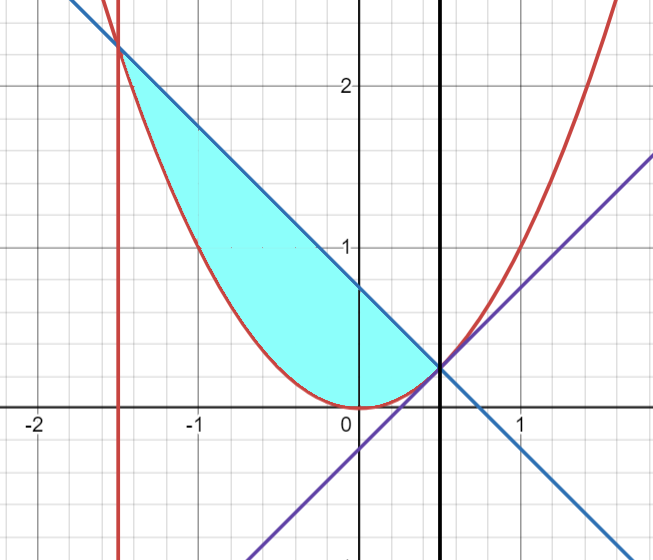
Did you manage to find the solution? How fascinating was your thought process? Please share your insights in the comments; I’m eager to hear from you!

Math Puzzles Compilation

Discover an engaging collection of math puzzles on Medium, covering a variety of topics including Algebra, Geometry, and Calculus. Don't hesitate to share this with friends!

The first video showcases a captivating math puzzle titled "Time Puzzle | Math Puzzle - YouTube," which offers additional challenges for puzzle enthusiasts.

The second video, "Fiddler 2024/01/19 - Can you make it home in time for pancakes: a math puzzle - YouTube," presents another engaging math challenge that complements this article.

Thank you for taking the time to read this piece! If you found it insightful, please consider giving it a clap. Your support motivates me to create more educational content.

If you appreciate my work, a small gesture like buying me a coffee would mean the world to me. It’s a wonderful way to support my writing endeavors. Happy solving!