A Simple Illustration

Imagine you ask four friends to rate four different movies on a scale from 1 to 5, or zero if they haven't seen the movie. The resulting ratings might look like this:

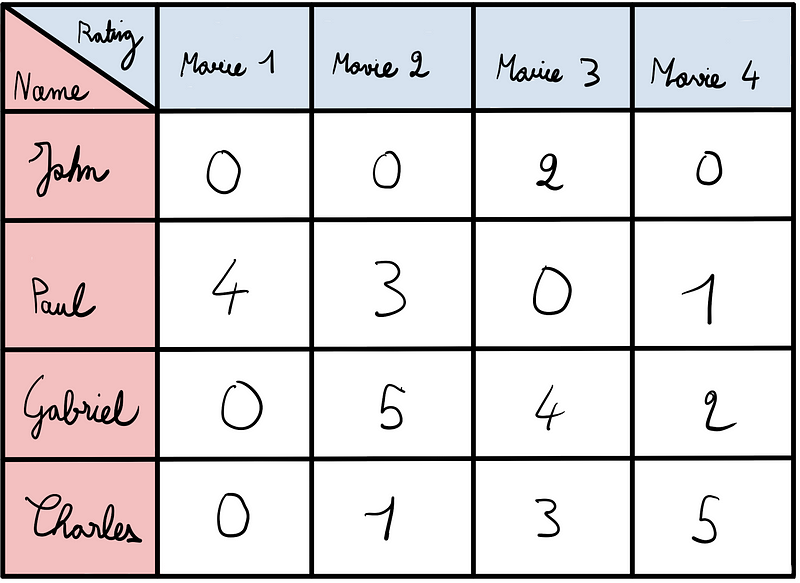
In this scenario, John has not watched movies 1, 2, and 4, but he rated the third movie with a score of 2. The sparsity of this matrix is relatively low, standing at 38% (6 zeros out of 16 total values), categorizing it as a "dense" matrix.

Now, consider a larger dataset, such as the 15,000 movies available on Netflix. Clearly, most users haven't seen all of these movies, resulting in a matrix largely filled with zeros.

Why Is This Important?

There are two main reasons to focus on sparse matrices: computational efficiency and storage optimization.

Storage of Sparse Matrices

Instead of storing every entry in a matrix, particularly those that are zero, it’s more efficient to only keep the non-zero values. For instance, if we only store the ratings of [1, 2, 4, 2, 1, 5, 1, 2, 3, 1] along with their respective positions, we eliminate the need to save all zero entries.

How is this done in practice? By utilizing the Coordinate list (COO) format, where we maintain three arrays: one for the values, one for their row positions, and one for their column positions.

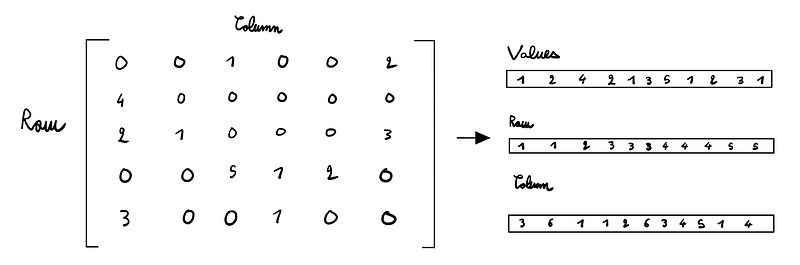
This method drastically reduces storage requirements. For instance, if you have a large dataset with 50 columns and 10,000 rows (500,000 values) but only 10,000 non-zero entries, you save a substantial amount of space.

Computational Complexity

The second advantage of sparse matrices lies in their computational efficiency during calculations. For example, when multiplying a vector by a sparse matrix, only the non-zero values contribute to the result.

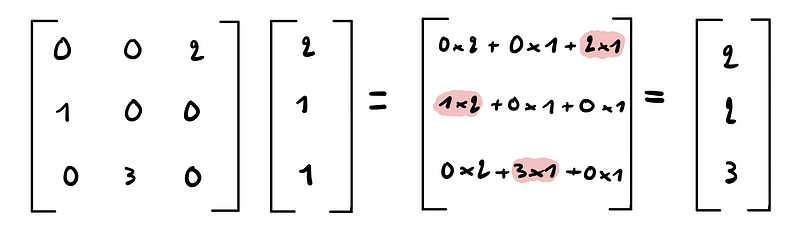
This means we can avoid unnecessary calculations with zeros, making the process significantly more efficient. Most machine learning libraries are designed to handle sparse matrices effectively.

The Netflix Prize Example

From 2006 to 2009, Netflix hosted a competition to enhance its movie recommendation algorithm, providing a dataset of over 100 million ratings across nearly 480,000 users for about 17,770 films.

To predict user ratings for unseen movies, the data needs to be structured efficiently.

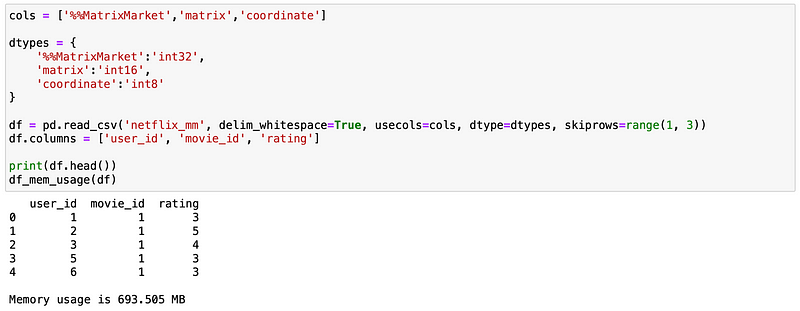
Given that most users have only seen about 150 films, the dataset turns out to be around 99% sparse after applying one-hot encoding.

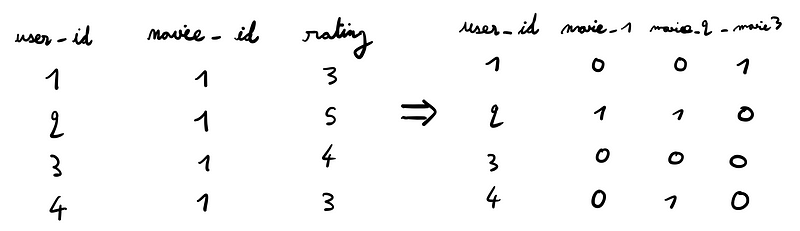
By using sparse arrays when performing one-hot encoding, we achieve a significant reduction in memory usage.

The memory footprint is now approximately 990MB, a substantial saving considering the volume of data.

Enhancing Scikit-Learn with Sparse Data

Utilizing sparse matrices can also streamline computations in machine learning algorithms. For instance, Scikit-learn provides sparse implementations for many of its classifiers, such as the Random Forest.

Employing sparse matrices can significantly reduce runtime, especially during resource-intensive tasks like Grid or Random searches.