Understanding Mathematical Problem-Solving Through First Principles
Written on
Chapter 1: Introduction to Triangular Triples
This content revolves around the Oxford University entrance exam question that exemplifies the systematic reasoning based on first principles, a method often utilized by proficient mathematicians and one that AI systems like GPT-4 find challenging.
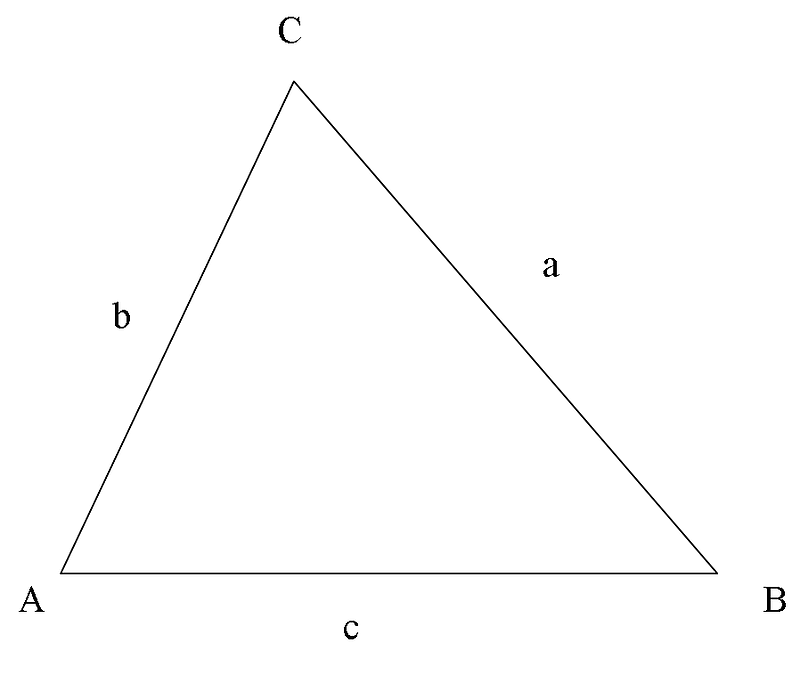
Most individuals are acquainted with the properties of right-angled triangles. According to the Pythagorean Theorem, for two shorter sides denoted as a and b, and the longest side c, the equation a² + b² = c² holds true. The integer solutions to this theorem are known as Pythagorean Triples, with classic examples being (3, 4, 5) and (5, 12, 13).
A broader concept is that of Triangular Triples. This term refers to any group of three positive integers that can represent the lengths of a triangle's sides. While integer Pythagorean triples are indeed triangular triples, the definition extends further: a set of integers (a, b, c) qualifies as a triangular triple if, when arranged in non-decreasing order, the sum of the two smaller integers exceeds the largest one.
For instance, consider the set (4, 2, 3). This can form a triangle since 2 + 3 > 4. Likewise, (2, 2, 2) is a triangular triple; however, (1, 3, 1) fails this criterion as it cannot form a triangle (1 + 1 ≤ 3).
A recent Oxford University problem addressed triangular triples and serves as an excellent illustration of how to deconstruct complex problems into manageable parts using first principles.
The problem introduces a function f(P) for P > 2, defined as the number of triangular triples summing to P. Specifically, it asks us to determine f(21). Though calculating the number of triangular triples summing to 21 may seem daunting, a systematic approach reveals a simple solution. Additionally, I will demonstrate that AI, such as GPT-4, often struggles with questions requiring this foundational reasoning.
Here are the problem's components and my solutions, which I found both intriguing and a valuable exercise in mathematical reasoning requiring minimal textbook knowledge.
Section 1.1: Initial Calculations
- Calculate f(3), f(4), f(5), and f(6).
This part familiarizes us with the concept. The only positive integer triple that sums to three is (1, 1, 1), which is a triangular triple, thus f(3) = 1. For a sum of 4, the integers must include 2, but since (1, 1, 2) does not satisfy the triangular condition, f(4) = 0. Analyzing the sum of 5, the integers must involve either 2 or 3. The configurations (2, 2, 1), (2, 1, 2), and (1, 2, 2) qualify as triangular triples, leading to f(5) = 3. Lastly, for f(6), the only valid triangular triple is (2, 2, 2), giving f(6) = 1.
The first video, "Differentiation from First Principles - HOW TO GET THE MARKS IN YOUR A-LEVEL EXAM," elaborates on the foundational techniques essential for mastering differentiation.
Section 1.2: Proving Properties of Triangular Triples
- For any triangular triple (a, b, c), demonstrate that (a+1, b+1, c+1) is also a triangular triple.
Assuming a, b, c are in non-decreasing order, we can derive that (a+1) + (b+1) = (a+b) + 2 > c + 2 > c + 1. Hence, (a+1, b+1, c+1) forms a triangular triple.
- If (x, y, z) is a triangular triple and x+y+z is even and at least 6, show that x, y, z are all at least 2, and that (x-1, y-1, z-1) is also a triangular triple.
Assuming x, y, z are arranged in increasing order, we need to prove that x cannot equal 1. If x = 1, then y+z must be odd, contradicting the initial condition of evenness. Thus, x must be greater than 1.
Section 1.3: Establishing Relationships Between f(P)
- For any positive integer k ≥ 3, show that f(2k-3) = f(2k).
By the previous proof, we know that each triangular triple summing to 2k-3 can be uniquely mapped to one summing to 2k by adding 1 to each number, meaning the counts of both sets must equal.
- Let S ≥ 3 and P = 2S. Show that (a, b, c) is a triangular triple summing to P if and only if each of a, b, c is strictly less than S.
We will prove this in both directions, establishing that if a+b > c, then c must be less than S, and vice versa.
- For any a with 2 ≤ a ≤ S-1, show that the number of valid b values such that (a, b, P-a-b) is a triangular triple is a-1.
Based on the previous findings, we can conclude that for a specific value of a, b can take values ranging from S-a+1 to S-1, yielding a total of a-1 possible values.
- Derive an expression for f(P) for any even P that is at least 6.
Let (a, b, P-a-b) be a triangular triple. Since a can range from 2 to S-1, and for each a, there are a-1 valid b's, we can formulate f(P) based on these parameters.
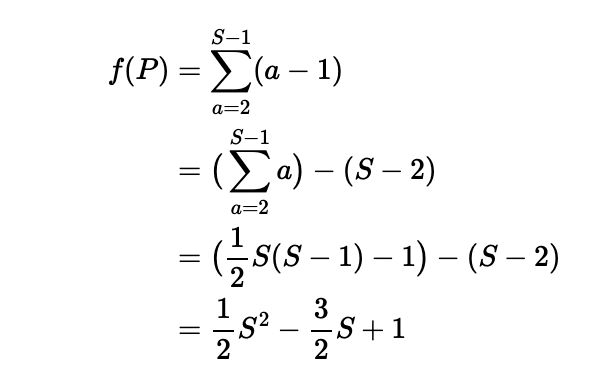
- Calculate f(21).
Using the result from (iv), we find that f(21) = f(24). Since 24 is an even number greater than 6, we apply our established formula, with S set to 12, yielding a total of 55.
To validate this, I also created a simple counting function in R:
n_triangular_triples <- function(P) {
check <- c()
for (a in 1:P) {
for (b in 1:(P - a)) {
if (P - a - b > 0) {
sorted <- sort(c(a, b, P - a - b))
if ((sum(sorted) == P) && (sorted[1] + sorted[2] > sorted[3])) {
check <- append(check, 1)}
}
}
}
sum(check)
}
By running this function for P = 21, the output confirms the count:
[1] 55
Additionally, we can use our formula to compute f(P) for larger values. For instance, f(997) = f(1000) = 124,251. The verification through the R function takes a bit longer, but it provides reliable results.

Despite GPT-4's attempts to elaborate on the Triangle Inequality Theorem, its answers varied significantly, highlighting the importance of true comprehension in mathematics.
What are your thoughts on this problem? I welcome your comments.