Today's Challenge

Our task is to demonstrate that the following set of vectors exhibits linear dependence:

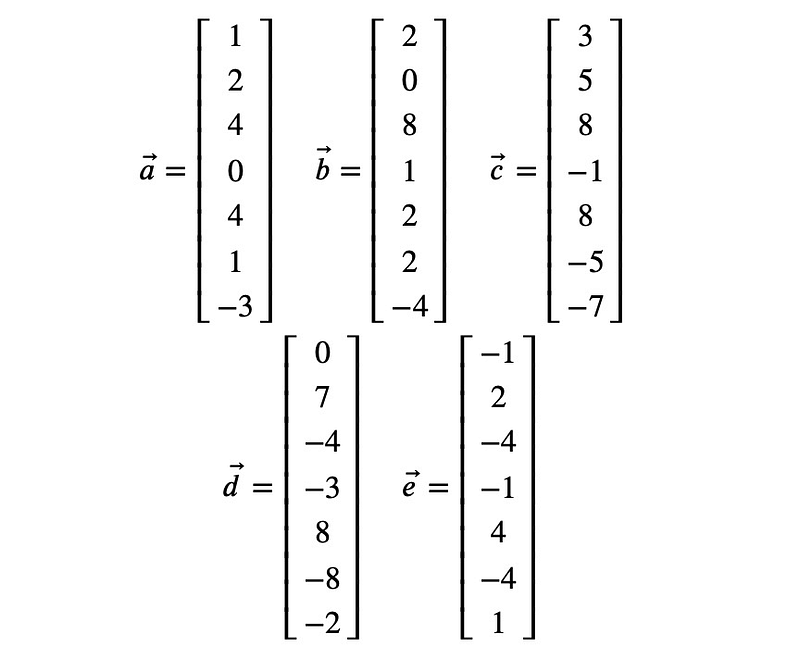
Next, we need to identify which vector(s) should be removed to ensure the remaining vectors are linearly independent.

Solution Using SymPy

To begin, we define our vectors:

The approach involves assembling these column vectors into a matrix and calculating its row-echelon form. If the row-echelon form is diagonal with only ones, the vectors are independent; otherwise, they are dependent.

We can create a simple helper function to combine column vectors into matrices:

Now, let’s verify that the five vectors are indeed linearly dependent:

The results indicate that this matrix is not diagonal, confirming the presence of linear dependence.

To determine which vector(s) contribute to this dependence, we can construct the set from the beginning, starting with two vectors:

This configuration is diagonal, suggesting that these two vectors are linearly independent.

Next, we proceed to add more vectors:

They remain independent at this stage. Continuing on:

At this point, the matrix is no longer diagonal, indicating that this vector can be expressed as a linear combination of the previous ones. Thus, we will exclude it and move forward:

Ultimately, the remaining vectors form a set of linearly independent vectors.

The first video titled "How to Determine if a Set of Vectors is Linearly Independent" provides further insights into this topic, offering a visual explanation of the criteria for linear independence.