# Understanding Inductive Bias in Machine Learning
Written on
Chapter 1: Introduction to Inductive Bias
In our previous discussion, we examined the concept of Empirical Risk Minimization (ERM). Today, we will delve into a challenge associated with this method.
When utilizing ERM, the ideal loss on the training dataset could theoretically reach zero. To accomplish this, the process involves:
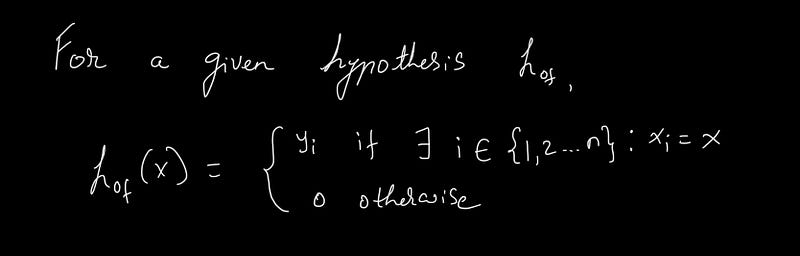
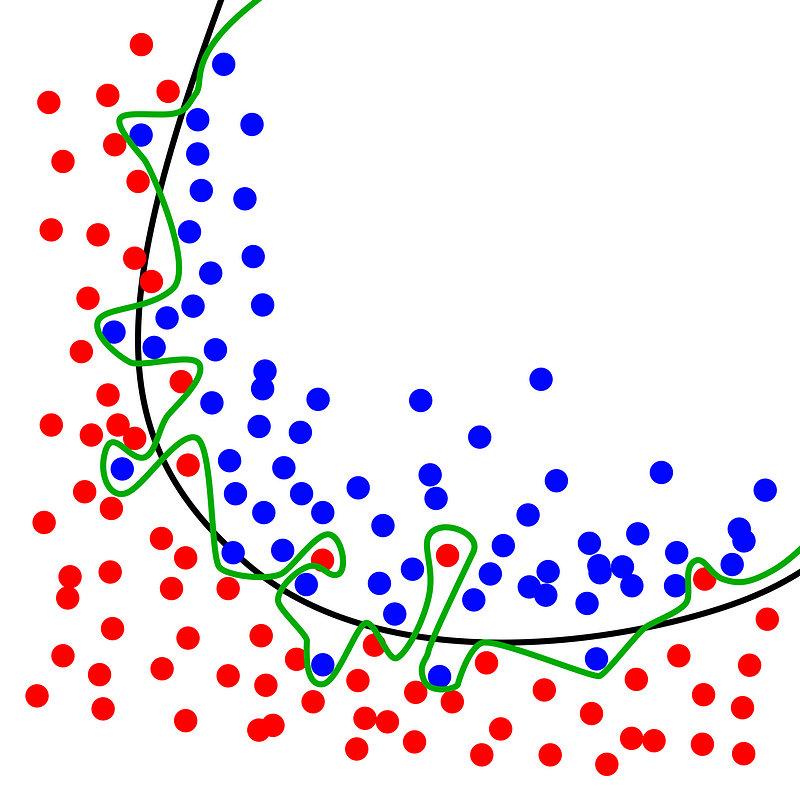
Imagine categorizing every papaya as 0 (not tasty) by default. If an example from the training dataset appears, you assign it the label Yi, which represents the true label available through supervised learning. This method allows for achieving zero loss as the algorithm matches every sample based on existing knowledge. However, the drawback arises when the algorithm cannot generalize effectively. While it may accurately predict familiar data, it struggles significantly with unseen examples, leading to what is known as Overfitting in machine learning. The fitting curve in the preceding illustration demonstrates this issue, as it aligns perfectly with the training data, yet we aim for a more generalized solution.
Section 1.1: Overfitting Explained
What does overfitting intuitively signify? Consider being shown images of various birds in flight and on the ground, with the instruction that all birds can fly. Initially, you are trained to label every bird as capable of flight (1). However, when faced with new images of different birds and other animals, you must discern which can actually fly. For instance: Sparrow? Flies. Lion? Does not fly. Crow? Flies. Elephant? Does not fly. Eagle? Flies. Penguin? Flies. Ostrich? Flies. Clearly, penguins and ostriches are grounded, and to amend this misconception, additional training with new data points—indicating these birds cannot fly—would be necessary. This iterative process continues with other flightless birds like emus and cassowaries. The question arises: how long can this cycle be sustained? Is it even practical?
A straightforward solution involves formulating a hypothesis: "Most birds can fly, but some cannot." With this assumption, you can reevaluate the training data and recognize that, despite being a bird, an ostrich is not capable of flight due to this flexible reasoning. This assumption, referred to as Inductive Bias in machine learning, allows for the inclusion of various assumptions within the learning paradigm.
Video Description: This video explains the concept of inductive bias in machine learning and its relevance to model generalization.
Section 1.2: Human Learning Analogy
Comparing this to human learning, I often form theories about new concepts and assess how additional information fits into my understanding. If new data aligns with my theory, I retain it; if not, I adjust my perspective. Philosophically, overfitting resembles a form of prejudice. Once rigid beliefs take root, learning is stifled (a nod to neuroplasticity—any neuroscientists, feel free to weigh in). Being excessively entrenched in a singular belief hampers generalization and distorts reality. Inductive Bias facilitates the filtering of noise from data, promoting open-mindedness and adaptability.
In machine learning terminology, we denote Inductive Bias as h ∈ H, indicating that any hypothesis h is selected from a broader set of hypotheses H. Continuing the analogy, the class H embodies all possible mental frameworks that can be applied to fit the data. If a hypothesis proves largely consistent, it is retained; if not, it is discarded or modified. To encapsulate this idea, I would like to quote my favorite author, Sir Arthur Conan Doyle, through the words of his character, Sherlock Holmes:
“It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts.”
With data at hand, our goal is to refine our theories to align with those facts, thereby emphasizing the necessity of Inductive Bias.
Chapter 2: Further Insights into Inductive Bias
Video Description: This video discusses inductive bias in machine learning, highlighting its importance in model training and generalization.