Origins of Fundamental Mathematical Symbols

The symbols ‘+’ and ‘-’ trace their roots back to Latin. Originally, the terms “p?” (più) for addition and “m?” (meno) for subtraction were used. In 1489, Johannes Widmann introduced the ‘+’ and ‘-’ symbols in his work aimed at merchants, where the former signified ‘surplus’ and the latter indicated ‘deficit’.

Robert Recorde, recognized for formalizing these symbols, sought a more efficient way to express equality. Tired of repeatedly writing “is equal to,” he created the ‘=’ symbol using two parallel lines.

The division symbol ‘÷’ is known as the obelus, first appearing in Johann Rahn’s algebra book “Teutsche Algebra.” Before its adoption for division, it was sometimes used to denote subtraction.

The multiplication symbol ‘×’ was notably used in John Napier’s “Mirifici Logarithmorum Canonis Descriptio,” with contributions from William Oughtred.

The first video provides insights into the origins of mathematical symbols, exploring their historical context and evolution.

Modern Mathematics: A Symbolic Challenge

Having traced the origins of key symbols, we must consider why mathematicians opted for such representations. The truth is, mathematicians, like many people, seek efficiency.

Imagine having to write “is equal to” a hundred times in an hour. Would you not prefer a shortcut? This quest for conciseness is at the heart of mathematical symbols, which serve to compress complex ideas into manageable forms.

If mathematicians relied solely on words, the content currently fitting on a single page could easily expand to multiple pages, potentially leading to confusion.

However, this symbolic compression is not without its issues. Before exploring these challenges, let’s take a look at some examples of contemporary mathematical symbols.

Examples of Modern Mathematical Symbols

Consider the following mathematical expression:

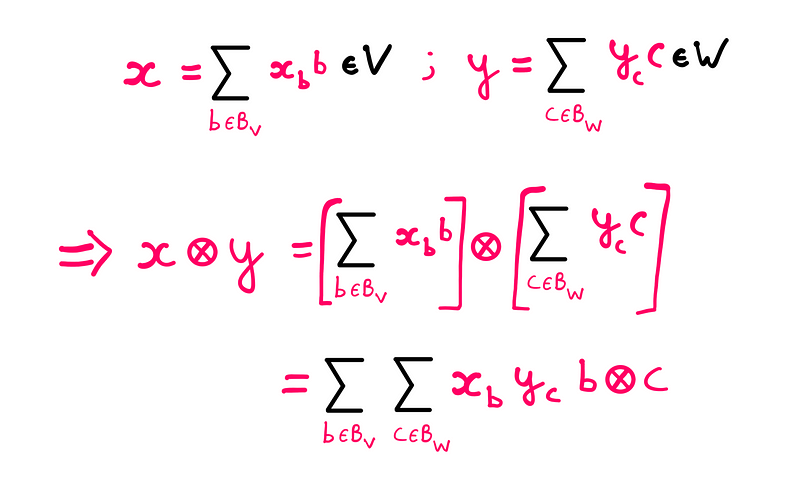
This image illustrates the tensor product of two vectors, showcasing how symbols can become increasingly complex. The circle with a cross inside it denotes the tensor product, reflecting the ongoing evolution of mathematical language.

As new fields emerge, fresh symbols are often created, leading to potential confusion when the same symbol carries different meanings in different contexts.

Mathematics: A Living Language

Mathematics is not a static discipline; it constantly evolves as researchers push its boundaries. This growth means that new symbols continuously emerge, making it difficult for any single mathematician to master the entirety of mathematical language.

As more concepts and symbols are developed, the challenge of understanding mathematics as a whole becomes increasingly daunting. The growth of symbols appears limitless.

Is this a genuine problem, or am I overly pessimistic? What direction should mathematics take moving forward?

A Possible Resolution

The core issue arises when students perceive “mathematics” as a subject that can be fully mastered. While individuals can reach a high level in specific sub-fields, the overarching body of mathematical knowledge is ever-expanding and likely beyond the grasp of any one person.

It may be beneficial to define symbols and their meanings clearly within specific sub-fields, allowing for reuse across different areas while maintaining context. This could help reduce confusion but may also lead to conflicts between meanings in interdisciplinary studies.

Final Thoughts

While I do not claim to have all the answers, I hope to spark discussion about the organization of mathematical symbols. Some researchers are already implementing similar ideas, and a more structured approach could prevent both experts and novices from feeling overwhelmed in the expanding field of mathematics.

As this discipline continues to grow, it could become less accessible to students, posing a significant challenge for future generations.

If you wish to support my work, consider contributing on Patreon.

You can explore my entire body of work on my about page.

The second video examines the importance of mathematical language and symbols, discussing their role in contemporary mathematics.