Chapter 1: Introduction to Matrix Multiplication

When faced with two real n x n matrices A and B, the task is to compute the resulting n x n matrix C = AB, which represents the product of A and B. We denote the element in the i-th row and j-th column of matrix A as a(i,j), with similar notations for matrices B and C. Consequently, the element c(i,j) of matrix C can be expressed as follows:

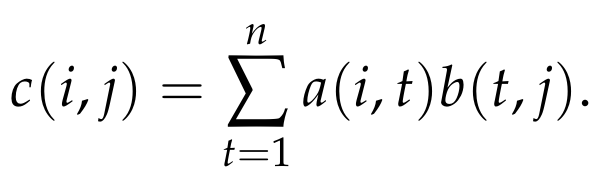
A natural question arises regarding the computational time required to derive matrix C. By examining the definition above, we can easily devise a basic algorithm, which we can outline in pseudo-code:

INPUT: n x n matrices A and B

OUTPUT: the n x n product matrix C = AB

for i = 1,...,n:

for j = 1,...,n:

c(i,j) = 0;

for t = 1,...,n:

c(i,j) = c(i,j) + a(i,t) * b(t,j);

return C;

Assuming constant time for additions, multiplications, and memory access, it's clear this algorithm performs approximately n³ operations, given its three nested loops. Thus, its time complexity is Θ(n³).

While polynomial-time algorithms for matrix multiplication exist, the frequent practical applications of matrix products prompt the search for more efficient algorithms.

To this day, determining the precise time complexity of Matrix Multiplication remains a significant open question in Theoretical Computer Science.

Chapter 2: Strassen’s Algorithm

This section focuses on Strassen's algorithm, which was the first to surpass the O(n³) time complexity barrier. Developed by Volker Strassen in 1969, this method employs a clever Divide-and-Conquer approach that enhances running time efficiency.

For simplicity, we will assume n = 2^k for some positive integer k. This assumption is valid since we can always pad matrices A and B with additional zero rows and columns, ensuring that the new n remains close to the original value.

To illustrate, let’s express matrices A, B, and C as block matrices:

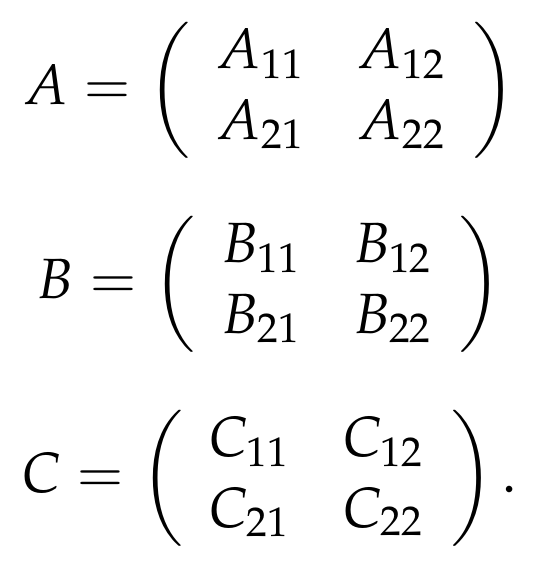
Each sub-matrix in this configuration has dimensions (n/2) x (n/2). The following equations can be derived:

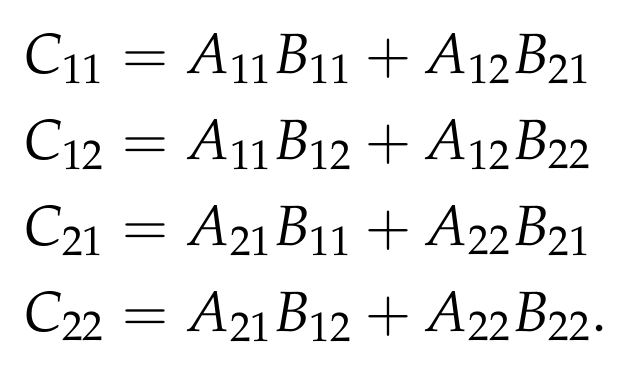
From these equations, a straightforward recursive algorithm can be formulated. We would recursively calculate the eight products of (n/2) x (n/2) matrices as indicated in the four equations and, in O(n²) time, sum all results to yield the final matrix C. The running time T(n) for this recursive method is defined by:

T(n) = 8 T(n/2) + O(n²).

Applying the Master Theorem, we see that this recursive algorithm maintains a running time of T(n) = O(n³), indicating no advancement in efficiency.

However, Strassen's innovation lay in reducing the number of recursive calls from 8 to 7, resulting in a new recursive algorithm with a running time S(n):

S(n) = 7 S(n/2) + O(n²).

This adjustment leads to significant implications.

The first video titled "Strassen's Algorithm for Matrices - Divide and Conquer" provides a comprehensive overview of this revolutionary technique.

Strassen's Insight

Strassen made an insightful observation by defining several matrices:

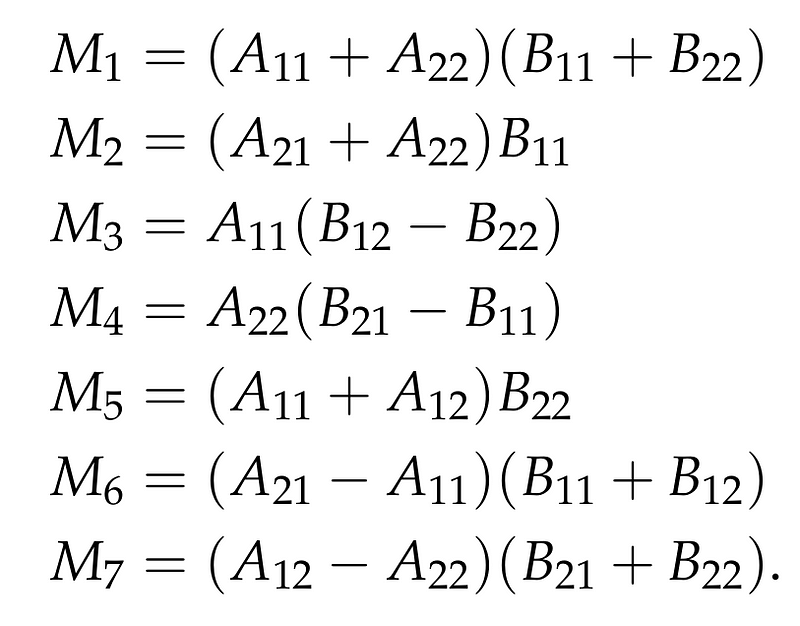
These matrices may seem arbitrary at first glance, but through careful manipulation of the expressions defining the four blocks of C, Strassen ingeniously arrived at these definitions. Notably, each matrix M can be computed with a single recursive call, leaving the remaining operations as additions. This allows for seven recursive calls to be sufficient.

Strassen confirmed that the following equations hold:

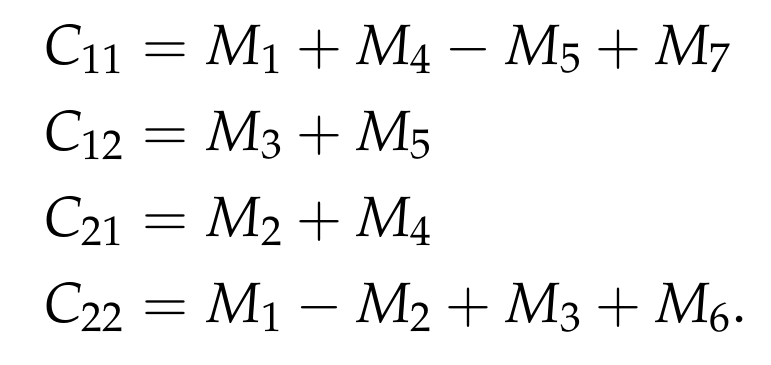
Verifying these equations is straightforward; we can confirm the second equation and leave the rest as an exercise for the reader.

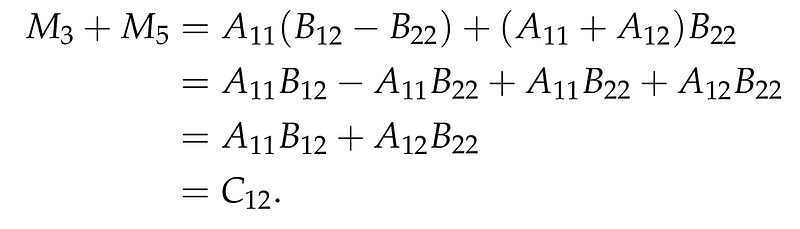
Given that the number of matrix additions required is constant, the overall complexity aside from recursive calls is O(n²). Therefore, we conclude:

S(n) = 7 S(n/2) + O(n²).

Conclusion

Strassen's algorithm marked a pivotal advancement in computational methods and initiated extensive ongoing research. The primary open question is whether a Matrix Multiplication algorithm exists with a time complexity of O(n²). Given that the size of both input and output is n², this represents a clear lower bound. The constant in the exponent of the optimal Matrix Multiplication algorithm is denoted as 𝜖, with current estimates ranging from 2 to approximately 2.8074. The latest advancements by Francois Le Gall suggest that 𝜖 is less than 2.3729.

A visual representation of the progress in 𝜖 over the past fifty years can be seen below:

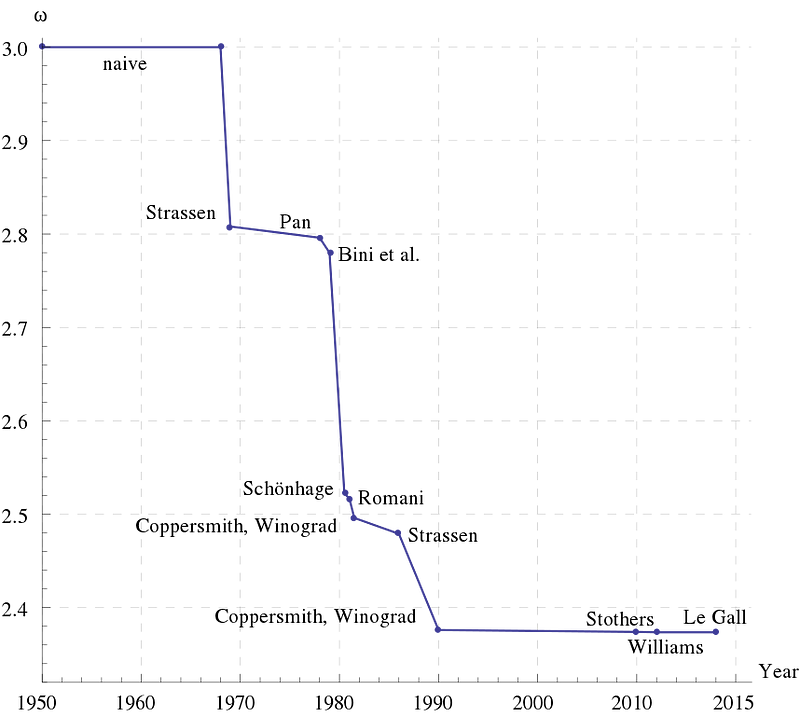
The future will ultimately reveal whether 𝜖 equals 2 or if there exists an inherent structural limitation to achieving this target.

References

The second video, "Strassen's Matrix Multiplication by Divide and Conquer," further elaborates on this innovative algorithm.