Step 1: Defining Transcendental Numbers

A transcendental number is defined as one that cannot be expressed as the root of any polynomial with integer coefficients. In contrast, numbers that are roots of such polynomials are termed algebraic.

Interestingly, while proving the existence of transcendental numbers is relatively straightforward, demonstrating that a specific number is transcendental is quite complex. For example, the square root of 1.5 is not transcendental, as it satisfies the equation 2x² - 3 = 0. On the other hand, π (pi) is indeed transcendental because no integer-coefficient polynomial has it as a root, although proving this fact requires the sophisticated Lindemann-Weierstrass Theorem.

Let’s address an unusual question: we aim to show that transcendental numbers exist without needing to provide a specific example!

A Note on Terminology:

1. I will sometimes use the term algebraic equations to refer to polynomials with integer coefficients.
2. A countably infinite set includes an infinite number of elements that can be enumerated. Formally, we can pair these elements with positive integers, allowing us to identify each element's position in the list.

Step 2: The Countability of Algebraic Numbers

It’s important to note that the set of algebraic numbers is countably infinite. This means we can theoretically create a list where any algebraic number can be pointed out by its position.

To clarify, let’s consider the integers, which are also countably infinite. For example, the sequence (0, -1, 1, 2, -2, 3, -3, ...) continues indefinitely. If you provide me with a number, such as 50 or -10, I could eventually find it at a finite position in that list.

Countable Pairs of Integers:

Imagine a large grid filled with people. We can count them in various ways: by columns, rows, or diagonals. However, with an infinite grid, counting down one of the columns means you would never reach the end. This indicates an abundance of people, but it doesn’t prove that we can list all of them.

Instead, we can count along the diagonals, where each diagonal contains a finite number of people.

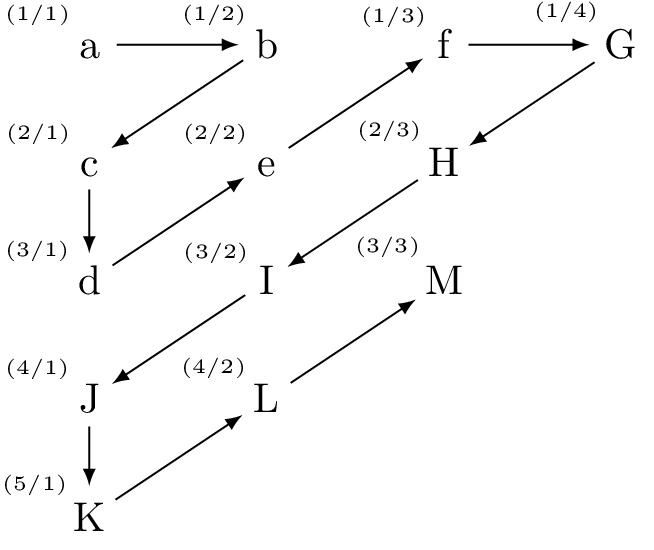
This method confirms that the pairs of integers are countably infinite. If you present me with a pair of integers, it corresponds to a point in the grid located in some diagonal.

Step 3: Uncountability of Real Numbers

Now, let’s demonstrate that there are uncountably many real numbers. Suppose someone claims to have a complete list of all real numbers. You can easily prove them wrong by constructing a number that isn't on their list.

To do this, you would look at the first number on their list and choose the first digit in the tenths place to be different from theirs. For the hundredths place, you would do the same, and you can continue this process indefinitely.

Thus, there is no way to compile a list that includes all real numbers.

Conclusion: The Existence of Transcendental Numbers

By combining our previous findings, we conclude that there are transcendental numbers! We’ve shown that algebraic numbers are countably infinite, meaning we can construct a list containing all of them. However, there is no way to create a countably infinite list that includes all real numbers. This means our list of algebraic numbers must omit many real numbers, confirming the existence of an uncountable number of transcendental numbers.

Congratulations on grasping Cantor’s diagonalization argument—a significant advancement in 19th-century mathematics that applies to the fascinating realm of transcendental numbers!