COVID-19 Testing: Understanding False Positives, Negatives, and Bayes' Rule
Written on

Note from the editors: Towards Data Science is a Medium publication focused on data science and machine learning. We are not health experts, and the views in this article should not be considered professional advice. For more information on the coronavirus pandemic, click here.
Note from the author: As a semiconductor technologist, my interest lies in applying data science and machine learning to relevant challenges in my field. I do not possess expertise in medicine or epidemiology. Please refrain from sending related inquiries.
What Are False Positives and Negatives?
Medical tests, like those for COVID-19, provide binary outcomes—either positive or negative. However, several questions arise:
- Can you trust the result completely?
- Is the likelihood of error greater for positive results compared to negative ones?
- What are the consequences of a mistake? Are they equal for 'YES' and 'NO' results?
- Should you undergo multiple tests to ensure accuracy? Is this more relevant for a 'YES' or 'NO' outcome?
No test is infallible. Reports indicate a significant variation in the accuracy of rapidly developed COVID-19 tests, and the term ‘accuracy’ has a precise definition in the context of medical assessments.
Test Outcomes Explained
Consider four scenarios regarding test results for a specific individual:
- You are infected, and the test is TRUE POSITIVE (TP).
- You are not infected, but the test shows FALSE POSITIVE (FP).
- You are not infected, and the test gives a TRUE NEGATIVE (TN).
- You are infected, but the test results in FALSE NEGATIVE (FN).
From a personal standpoint, I would prefer a test that accurately identifies my condition. A high TP and TN rate ensures that the test serves its purpose, which includes accurately identifying non-infected individuals as negative.
Accuracy measures typically refer to the percentage of correct results (TP and TN) relative to total tests conducted. However, high accuracy alone is insufficient; false positives and negatives also matter.
Different Costs of Test Outcomes

#### TRUE NEGATIVE (TN)
This is the most cost-effective scenario. After testing, you go home without stressing the healthcare system, incurring only the emotional cost of waiting for results.
#### TRUE POSITIVE (TP)
This scenario is concerning but not the worst. After being diagnosed as COVID-19 positive, you may need to self-isolate or seek hospitalization, each with different implications for you and the healthcare system.
#### FALSE NEGATIVE (FN)
This is the most serious scenario. An individual with COVID-19 goes untreated, which can lead to severe consequences, especially for those at higher risk.
#### FALSE POSITIVE (FP)
This situation burdens the healthcare system, as individuals without the virus may be treated as positive, misallocating resources and causing unnecessary emotional distress.
Statistical Insights
Such binary classification tests are well-studied in statistics, often referred to in terms of Type-I and Type-II errors. The Confusion Matrix summarizes these outcomes.

Recent advancements in machine learning utilize such matrices to evaluate system performance, allowing for the calculation of various metrics from the basic outcomes.
Applying Bayes' Rule to COVID-19 Tests
Bayes' theorem, often regarded as a cornerstone of probability, helps update the likelihood of an event based on new information.
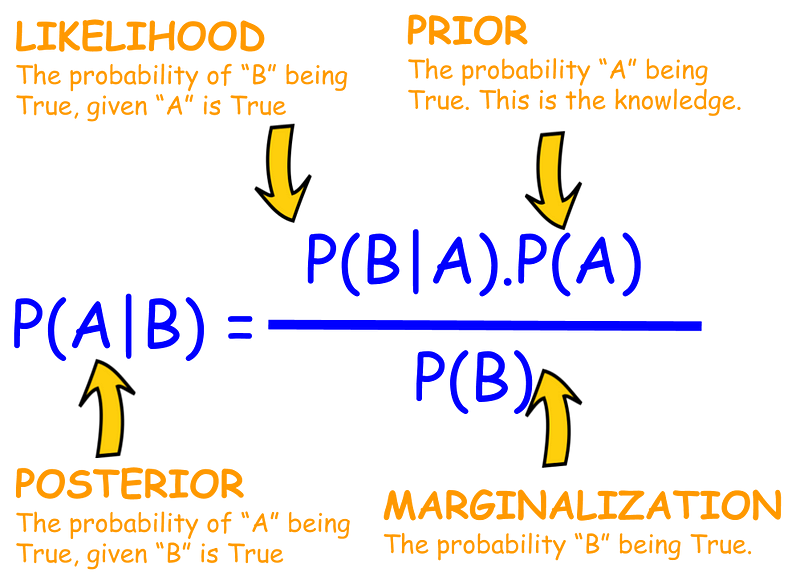
In medical contexts, this updating process means we continuously re-evaluate our assumptions based on test data, similar to seeking multiple medical opinions.
Practical Application of Bayes' Rule
To determine if a person is COVID-19 positive, we rely on the test results, yet we can only provide probabilities rather than certainties.
Let’s define some probabilities:
- P(COVID-19 positive | test = positive): The probability of actually being positive given a positive test.
- P(test = positive | COVID-19 positive): The test's sensitivity, or the rate of true positives.
- P(COVID-19 positive): The overall prevalence of the virus in the population.
- P(test = positive): The total probability of a positive test result, encompassing both true and false positives.
This Bayesian framework allows us to calculate the likelihood of infection based on testing outcomes.
Summary
We are experiencing the most significant global health crisis since World War II. As data scientists, we can leverage our skills in statistical modeling to analyze COVID-19 testing data critically.
The insights provided here emphasize the importance of understanding false positives and negatives in medical testing. Medical professionals regularly engage with these concepts, and it's crucial for us to share this knowledge effectively.
Stay safe and informed!
Note from the author: As a semiconductor technologist, my focus is on applying data science within my field. I lack medical expertise, so please refrain from sending related inquiries.
For questions or ideas, contact the author at tirthajyoti[AT]gmail.com. Visit the author's GitHub repositories for code, ideas, and resources in machine learning and data science. Connect with the author on LinkedIn or follow on Twitter for more insights.