Chapter 1: The Role of Technology in Learning Mathematics

In Melbourne, Australia, where I instruct high school math, students are permitted to utilize a CAS (Computer Algebra System) calculator during most of their math assessments. These calculators can solve equations, graph functions, perform differential and integral calculus, and even execute programming tasks!

To illustrate their capabilities, let’s examine a complex numbers question from our 2023 Specialist Mathematics Exams, which is the highest level of math offered. The question is as follows:

If ( z = a + bi ), where ( a, b in mathbb{R} ) and ( a > b > 0 ), what is ( text{Arg}(z + iz^*) )?

Without a calculator, one would need to adopt an algebraic method to solve this. We know that ( z^* ) (the conjugate of ( z )) is ( a - bi ). By multiplying this by ( i ) and simplifying, you can determine that the angle is the inverse tangent of 1, yielding 45° or ( frac{pi}{4} ) radians.

This approach requires considerable effort!

A geometric interpretation also exists. The conjugate reflects over the real axis, and multiplying by ( i ) results in a 90° counter-clockwise rotation. Therefore, the complex number ( iz^* ) has an angle of ( 90° - theta ), where ( theta ) is the angle of the original complex number ( z ). This indicates that ( z ) and ( iz^* ) are symmetrical about the line ( y = x ), and since they share equal magnitudes, their sum must fall on the line ( y = x ), which is 45° or ( frac{pi}{4} ) radians from the x-axis.

However, with a CAS calculator, this complexity diminishes! I can define ( z ) as ( a + bi ), utilize an angle function for complex arguments, and apply a conjugate function. Additionally, I can set constraints for ( a ) and ( b ) to ensure they remain positive, which eliminates the uncertainty about which quadrant the complex number resides in (as we know ( a > b > 0 ) from the question).

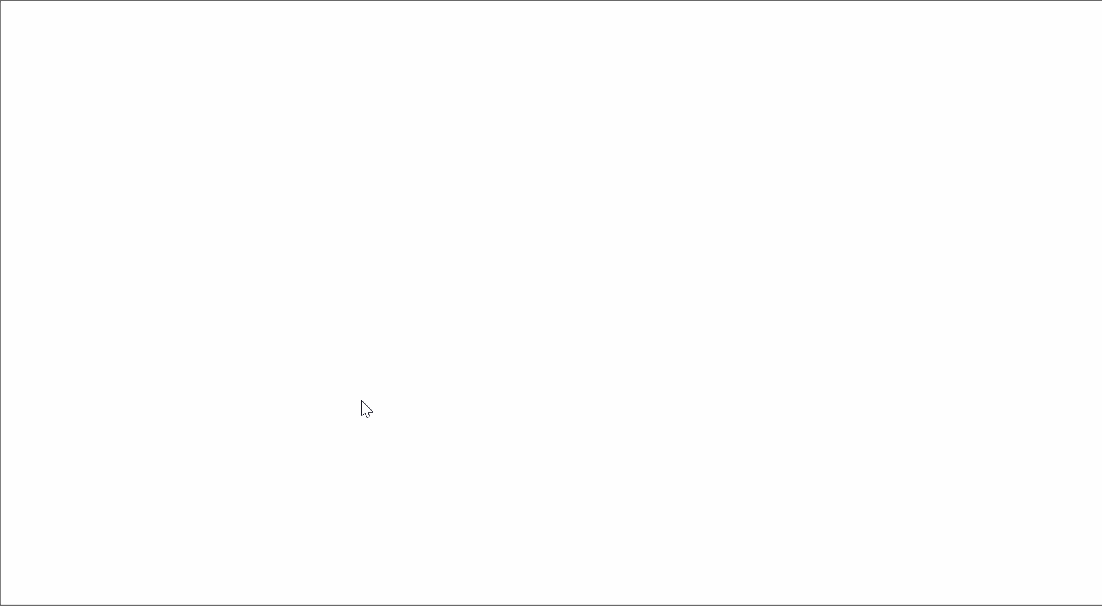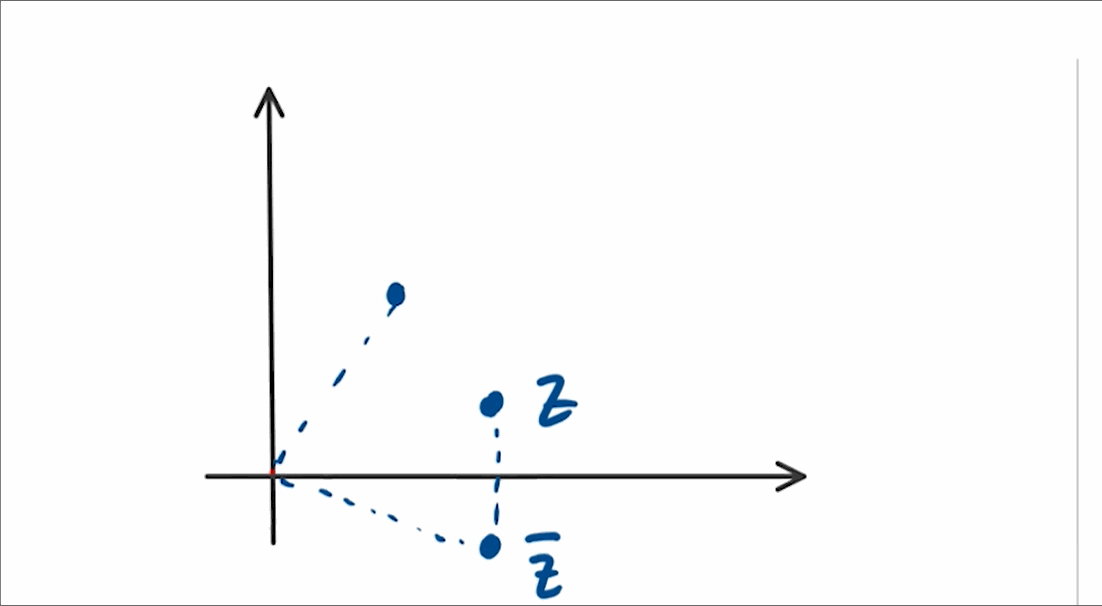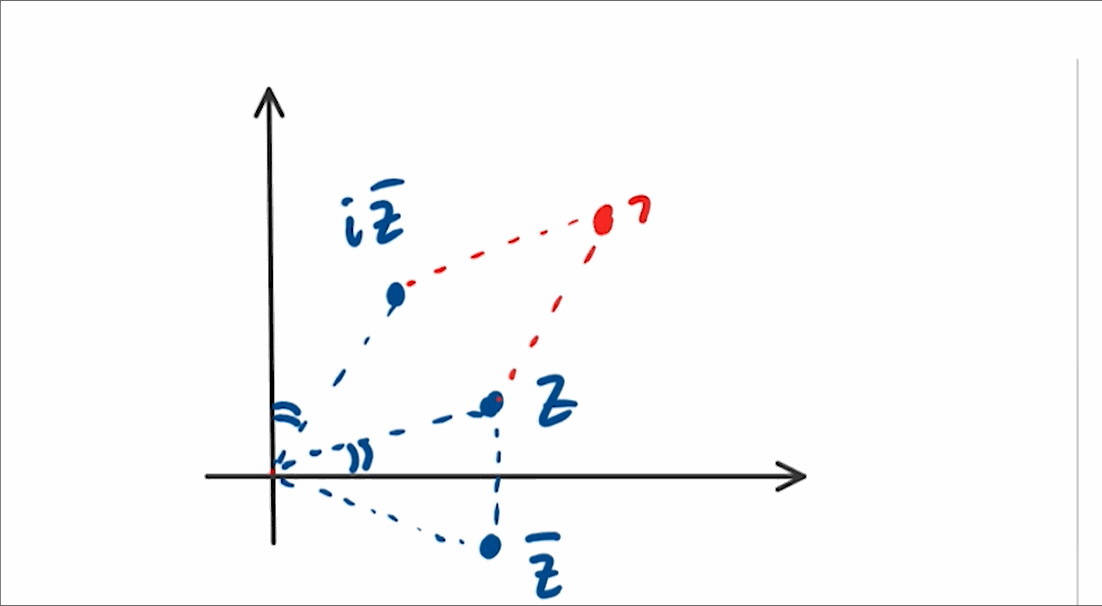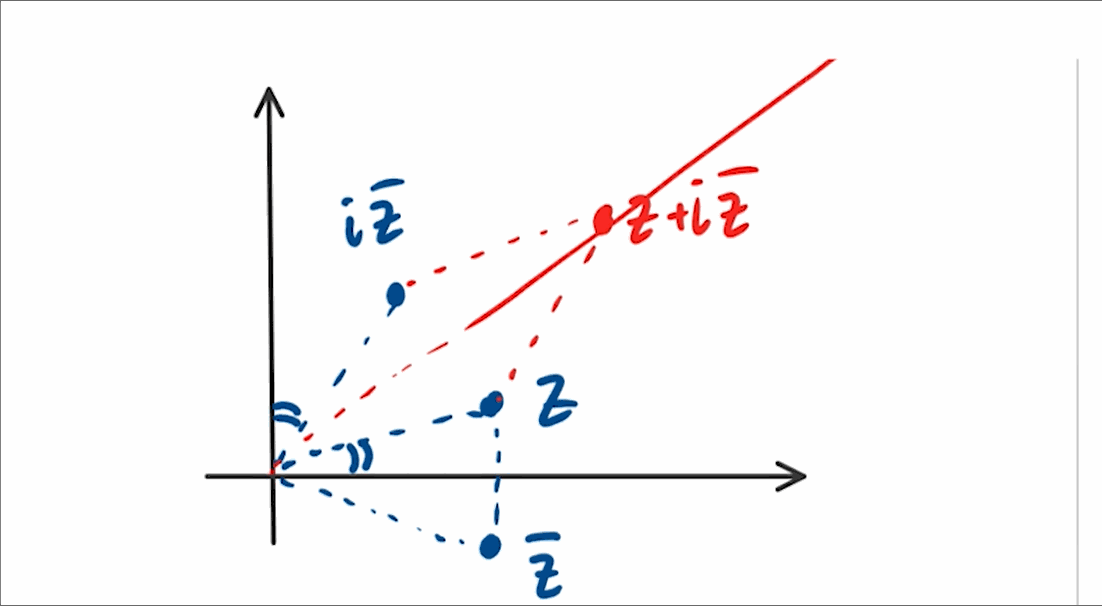
Impressive, right?

Before we delve into the discussion, it's important to note that not every student will be adept at executing the necessary calculator functions as demonstrated above. Mastery of these skills requires practice, much like learning programming syntax and conventions to solve problems effectively.

Moreover, Specialist Maths students must complete two exams: one allowing the use of a calculator and another without. The calculator exam, however, holds double the weight.

What are your thoughts? Has the calculator diminished the essence of mathematics? Or is technology now an integral component of math education that students should embrace?

Chapter 2: Exploring Complex Numbers with Video Resources

The first video titled "Scientific Calculator: Complex Numbers Operations (1) - YouTube" delves into the use of scientific calculators for handling complex number operations. It provides a step-by-step guide on effectively utilizing these tools to solve complex number problems.

In the second video, "How to solve Complex Numbers using Casio Calculator #jonahemmanuel #complexnumbers - YouTube," viewers are shown practical applications of a Casio calculator to tackle complex numbers, highlighting its functionalities in a clear and engaging manner.